Design of the BraKet Component
This is a collection of notes on the design of the classes for the BraKet component and should be formalized at some point.
In prototyping
BraKetandTensorRepresentationwere property types; however, this was burdensome when vector spaces/wavefunctions exhibited inheritance, e.g., if x inherits from y, then the property typeBraKet<y, Kinetic<Electron>, y>was different fromBraKet<x, Kinetic<Electron>, x>. Moreover because the latter property type did not inherit from the former, implicit conversion could not happen. WithBraKet(andTensorRepresentation) being traditional classes we can define our own implicit conversions easily.Rigorously kets are vectors and bras are operations which project onto a vector.
The “projection” part of the bra involves antilinear projection on to a vector. In practice, bras are labeled with the complex conjugate of the vector they project on to, i.e., if u is the complex conjugate of v than the bra which projects on to u is actually labeled v.
The points here being: one, we don’t expect the user to specify the projection, it’s implied, and two based on the labeling convention we need to internally take the complex conjugate of whatever the user gives us.
Following from the last points a bra-ket is rigorously a scalar; however, since this scalar is a tensor element it is also common to represent the entire tensor by specifying a generic element of the tensor in bra-ket form.
Think of \(\textbf{A}=\braket{i\mid A\mid j}\) as the analog of \(\textbf{A} = a_{ij}\).
From a design standpoint this means we want to be able to specify both an entire tensor and a tensor element with bra-ket objects. The two are distinguished based on whether the usr provides a specific vector or a generic vector (which we represent by the entire vector space it can stand for).
We have separate base classes for Wavefunction and VectorSpace. Should we have separate base classes for scalar vs tensor BraKets?
Users likely will expect “Wavefunction, Operator, Wavefunction” to evaluate to a scalar (or vector depending on the operator) and “VectorSpace, Operator, VectorSpace” to evaluate to a tensor.
Define
TensorRepresentationforBraKetthat evaluate to tensors andTensorElementforBraKetthat evaluate to an element of the tensor.Factor out common implementations into
BraKetBase.
TensorRepresentationandTensorElementcan be used to write generic drivers.Eventually
BraKetshould rely on a PIMPL to hold the state. PIMPLs can be used to optimize storage, e.g., only store the bra or the ket if its symmetricWe probably will need
BraKetViewto allow existing state to be used as if it were aBraKetwithout copying it.
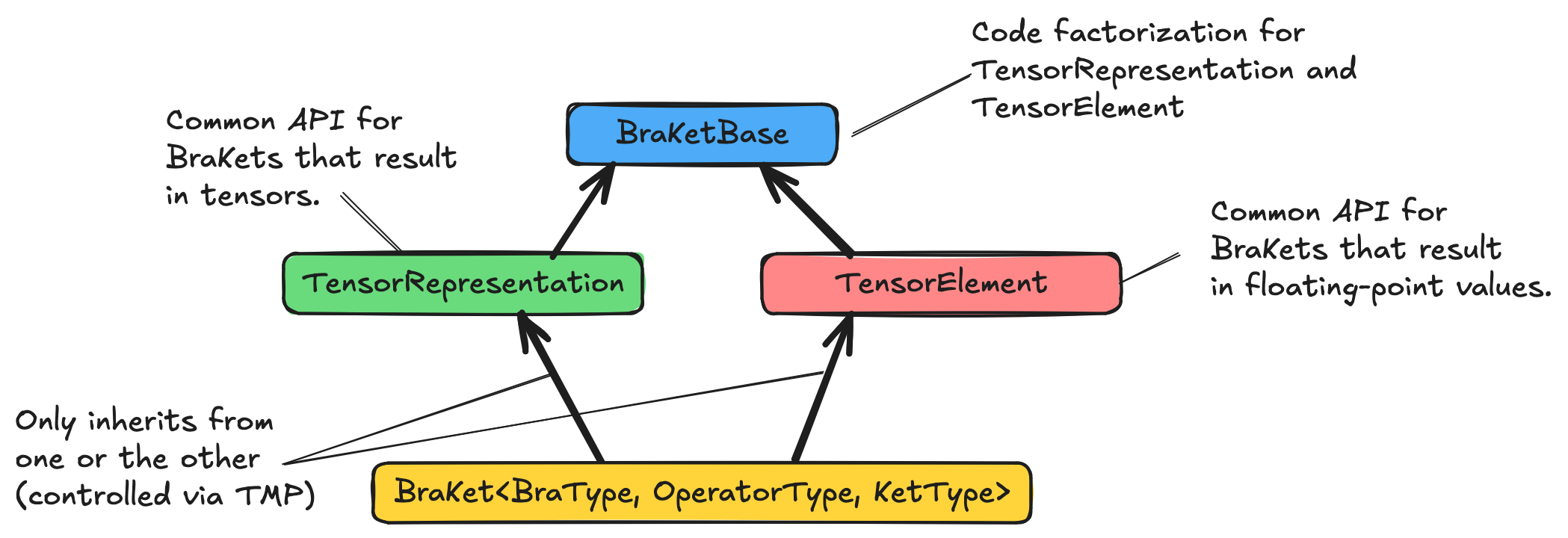
Fig. 17 BraKet class hierarcy.