Architecture of Operator Component
- The need for the Operator component stemmed from discussions on the
TODO: Write me!!!
Operator Consideration
- determinate vs. indeterminate
Most operators have a determinate form (i.e. a form that contains a set, well defined number of particles) and an indeterminate form (i.e., a form written in terms of a variable number of particles). Usually we refer to the indeterminate form as the “many-particle operator” and the determinate form as the “one-electron” (or “two-electron”) operator. Generally the indeterminate form is written as an indeterminate summation over determinate operators.
- care with template types
In composing operators we want to be able to write something like
2J - Kand have that result in the same type as-K + 2J.
Example Use Cases
The following pseudocode snippet is designed to show some high level examples of how we envision the operator component to be used. This snippet is used to motivate the design and may not actually represent the final version in Chemist.
// Operators in QM are defined in terms of particles. We start by making
// some particles. First for the one and two particle operators then for the
// many-particle operators. Creation of particles is the responsibility of
// the chemical system component
Electron e; // Electrons are indistinguishable, no need to make more.
Nucleus n0 = get_a_nucleus_object();
Nucleus n1 = get_a_different_nucleus_object();
ManyElectrons electrons(n_electrons);
Nuclei nuclei = get_many_nucleus_objects();
// Creates zero-electron operators
Kinetic<Nucleus> t_n(n0); // Born-Oppenheimer electronic structure won't use
Coulomb<Nucleus, Nucleus> v_nn(n0, n1);
// Create one-electron operators
Kinetic<Electron> t_e(e);
Coulomb<Electron, Nucleus> v_enucleus(e, n); // A piece of the next operator
Coulomb<Electron, Nuclei> v_en(e, nuclei);
// Create two-electron operator
// N.b. using the same particle is fine when the particles are wave-like,
// i.e., they don't have a set position
Coulomb<Electron, Electron> v_ee(e, e);
// The above operators allow us to go tensor element by tensor element.
// That's inefficient, but sometimes desired. In practice, we usually
// create many-particle operators
// N.b. for many particles providing the same object twice is allowed and
// the i != j restriction is understood.
Coulomb<Nuclei, Nuclei> V_nn(nuclei, nuclei);
Kinetic<ManyElectron> T_e(electrons);
Coulomb<ManyElectron, Nuclei> V_en(electrons, nuclei);
Coulomb<ManyElectron, ManyElectron> V_ee(electrons, electrons);
// Make the Hamiltonian for the entire system
Hamiltonian<ManyElectron, Nuclei> H(T_e + V_en + V_ee + V_nn);
// Extract pieces
CoreH<ManyElectron, Nuclei> Hcore = H.core();
ElectronicH<ManyElectron, Nuclei> Helec = H.electronic();
// Build (restricted) many-electron Fock operator
Density<ManyElectron> rho = get_one_electron_density();
Coulomb<ManyElectron, Density<ManyElectron>> J(electrons, rho);
K_HF<ManyElectron, Density<ManyElectron>> K(electrons, rho);
Fock<ManyElectron, Nuclei> F(Hcore + 2.0 * J - K);
// DFT
XC_KS<ManyElectron> XC(electrons, rho, /* enum defining the functional*/);
// Non-hybrid DFT
Fock<ManyElectron, Nuclei> K(Hcore + 2.0 * J + XC);
// Hybrid DFT (0.5 should be replaced with the appropriate fraction of
// exact exchange)
Fock<ManyElectron, Nuclei> K_hybrid(HCore + 2.0 * J - 0.5 *K + XC);
// Coulombic interaction with point charges
ChargeSet charges = get_some_point_charges();
Coulomb<ManyElectron, ChargeSet> V_eq(electrons, charges);
Design of the Operator Component
Note
Many operators are templated on T the type of particle contributing to
the operator. If T is the type of a class for a single particle (e.g.,
Electron or Nucleus) then the operator is a single-particle
operator. If T is the type of a class for an indeterminate number of
particles (e.g., ManyElectron or Nuclei) then the operator is a
many-particle operator. For operators involving more than one type of
particle the same logic applies to the other template parameters.
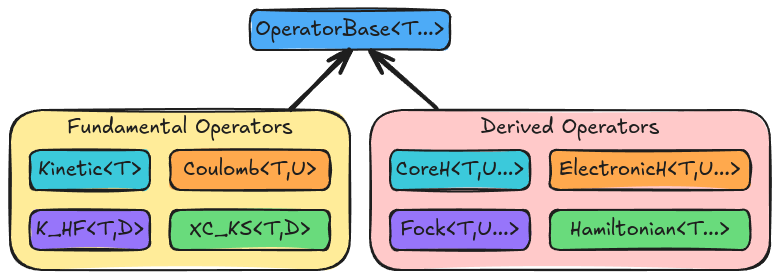
Fig. 16 Classes comprising the operator component of Chemist.
OperatorBase<T...>. This class is used to factor out common functionality, like holding/accessing objects of typeT, and also to store scale factors.
Fundamental Operators
Operators in this sub component are comprised of single interaction (though it may be over an indefinite number of particles).
Kinetic<T>. Describes the kinetic energy of a type of particle.Coulomb<T,U>. Describes the charge-charge interaction between particles. The particles may have the same type (T == U) or they may be different (T != U).K_HF<T,D>. Hartree-Fock exchange of a particle of typeTwith a density of typeD.XC_KS<T,D>. Kohn-Sham exchange-correlation operator for a particle of typeTwith a density of typeD.
Other potential operators include Dirac delta function, identity operator, and multipole moment operator.
Derived Operators
Note
The operator and wavefunction component will leverage the same set of classes for denoting operations.
Operators in this component are obtained by combining fundamental operators or other derived operators.
Hamiltonian<T...>. Represents the total Hamiltonian for the system. Can be decomposed into its various pieces.Fock<T, U...>. Represents an effective one-particle potential for a particle of typeTthat interacts with objects of typeU.... For Hartree-Fock this is the true Fock operator, for density functional theory this is the Kohn-Sham operator.ElectronicH<T, U...>. Pieces of the Hamiltonian that depend explicitly on electrons of typeT(assumed to be eitherElectronorManyElectron) interacting with objects of typeU.... Primarily a strong type to distinguish from the full Hamiltonian.CoreH<T,U,...>. Represents the exact Hamiltonian for a particle of typeTinteracting with objects of typeU....