Architecture of Wavefunction Component
The need for a wavefunction component was motivated in Architecture of the Quantum Mechanics (QM) Component.
What is the Wavefunction Component?
In the traditional view of quantum chemistry, the wavefunction represents the (possibly time-dependent) state of the system. Properties of the system are computed as tensor elements involving wavefunctions and operators. The Wavefunction component contains classes which facilitate the creation and manipulation of a chemical system’s wavefunction.
Why do we need a Wavefunction Component?
The wavefunction component is needed to express the state of the bra and ket and transfer that state to routines which evaluate tensor elements involving those bras and kets. It is also needed to facilitate the programmatic dispatching among electronic structure methods.
Wavefunction Considerations
- orbitals
Orbitals are the building blocks of many-particle wavefunctions. We need to be able to represent the set of orbitals from which the many-particle wavefunction is built.
- determinants and permanents
Determinants/permanents are the many-particle wavefunctions with the right spin symmetry for fermions/bosons respectively.
- basis function vs basis set
While the intermediates used to compute a property are often expressed as tensors, the property we want is often a single element of a larger tensor. We thus need a way to specify “compute the entire tensor representation” vs “compute the 0,0-th element”.
- implicit vs explicit
Some basis functions are typically explicit (e.g., atomic orbitals, molecular orbitals) meaning they have state which must be explicitly specified. Other basis functions are considered implicit (e.g., spin, Cartesian axis).
- method dispatching
One use of the wavefunction is to dispatch to different methods. For example, having different types for restricted vs unrestricted self-consistent field theory wavefunctions makes it easier to dispatch to RSCF/USCF respectively.
- bra/ket state
Aside from indicating the computation to do, the wavefunction will also be used to pass the parameters needed to describe the state of the bra or ket. Examples include:
AO basis set parameters.
molecular orbital coefficients
orbital occupations
Example Use Cases
The following pseudocode snippet is designed to show some high level examples of using the wavefunction component. It is not meant to be true to the final Chemist library (e.g., many of the typedefs exist as strong types for user ease), but simply motivational.
AOSpace aos(get_ao_parameters());
Spin spins(std::ratio(1, 2)); // Takes total spin of particle
// Can "slice" spaces to make subspaces
Spin alpha = spins.subspace(0, 1); // Spins count down
Spin beta = spins.subspace(1, 2);
// Spatial molecular orbitals (MOs) are formed by transforming AOs.
using MOSpace = Transformed<AOSpace>;
// Input is the transformation and the "from" space
MOSpace mos(c, aos);
// Spin atomic orbitals (SAOs) are products of AOs and spin
using SAOSpace = Product<AOSpace, Spin>;
// Input are the spaces to take the tensor product of
SAOSpace saos_alpha(aos, alpha);
SAOSpace saos_beta(aos, beta);
SAOSpace saos(aos, spins); //Union of saos_alpha and saos_beta
// Could have also obtained saos_alpha/saos_beta by slicing saos
// Could have also obtained saos by taking union of saos_alpha and saos_beta
// Transforming SAOs in general leads to spinors. Spin (molecular) orbitals
// (SOs) arise when coefficients can't mix spins
using SOSpace = Transformed<SAOSpace>;
SOSpace spinors(c_spinors, saos);
SOSpace so_alpha(c_alpha, saos_alpha);
SOSpace so_beta(c_beta, saos_beta);
SOSpace sos = so_alpha + so_beta; // Can treat the SMOs as a unified space
// Natural spaces diagonalize a quantity. Canonical means they diagonalize
// the Fock matrix
using CanonicalMOSpace = Natural<MOSpace>;
using CanonicalSOSpace = Natural<SOSpace>;
// Input is the diagonal elements and the orbitals
CanonicalMOSpace cmos(orbital_energies, mos);
CanonicalSOSpace csos(spin_orbital_energies, sos);
// For an n-particle system, orbital products of n orbitals are then
// antisymmetrized/symmetrized (for fermions/bosons respectively) to form
// n-particle basis functions
using RestrictedDeterminants = Antisymmetrized<CanonicalMOSpace>;
using UnrestrictedDeterminants = Antisymmetrized<CanonicalSOSpace>;
RestrictedDeterminants rdeterminant(n, cmos);
UnrestrictedDeterminants udeterminant(n, csos);
// By default the first n orbitals are used to form the reference state
// Can change the reference. This call for example sets the reference to
// orbitals 1 through n inclusive.
udeterminant.set_reference(1, 2, 3, ..., n);
// We rarely want the full space of determinants. We can limit our
// excitations by slicing the determinant space. Here we limit it to
// single and double excitations
auto singles = rdeterminant.excitation_subspace<1>();
auto doubles = rdeterminant.excitation_subspace<2>();
// More general slices can be accomplished by defining one or more active
// spaces. The argument is the orbitals involved in the active space (the
// class already knows whether those orbitals are occupied or not).
auto as = rdeterminant.active_space({10, 11, 12});
Design of the Wavefunction Component
Note
The design presently only includes classes which we plan to implement in version 1.0 of the wavefunction component.
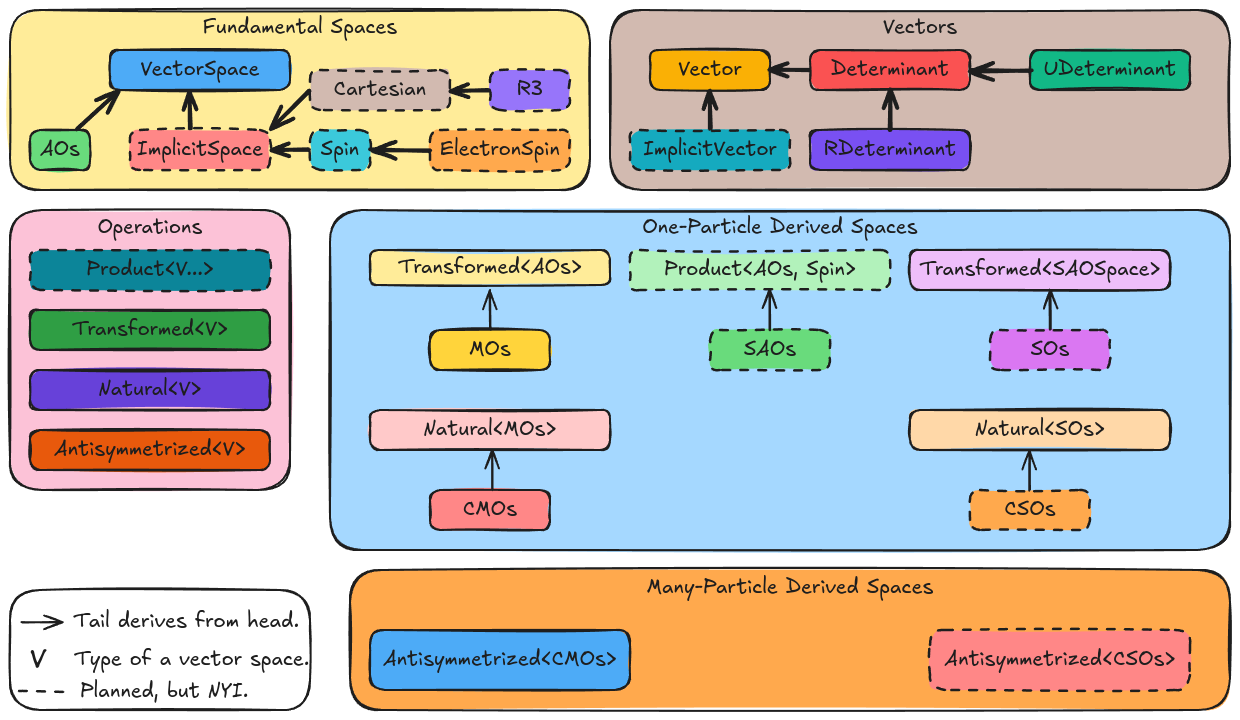
Fig. 15 Classes comprising the wavefunction component of Chemist. See documentation for class descriptions.
Fundamental Spaces
Note
We have opted to use the term “vector space” instead of “basis set” to avoid confusion with the more common practice of using “basis set” to refer to the parameters defining the atomic orbitals.
The classes in this sub-component of the wavefunction component represent the building blocks used to create the derived spaces via fundamental operations. Included in the fundamental spaces component are:
VectorSpace. Base class signifying that something is a set ofVectorobjects. Provides code-factorization for derived classes.AOs. Wrapper around anAOBasisSetobject. In order to conform to expectations, we made theAOBasisSetobject behave somewhat like the basis set objects found in other quantum chemistry programs. TheAOsclass is needed to make it interoperable with the wavefunction component.ImplicitSpace. Code factorization for implementing aVectorSpaceobject whose elements are implicit. Derived classes just need to define labels.Cartesian. Class defining an \(n\) dimensional Cartesian space. Code factorization for traditional \(\mathcal{R}^3\) as well as other spaces like \(\mathcal{R}^6\) (space where the unique quadrupole moment components live).Spin. Class defining the spin states for a particle given the particle’s total spin.R3. SpecializesCartesianto familiar “x”, “y”, “z” space.ElectronSpin. SpecializesSpinto the case of an electron’s spin, i.e., calls the spins \(\alpha\) and \(beta\) in accordance with usual practice.
Wavefunction
This sub-component of the wavefunction component contains classes defining
classes that represent objects that span a vector space. In practice these
objects are used to request a single element of a tensor via Dirac notation
whereas VectorSpace objects are used to request the entire tensor.
Wavefunction. Base class signifying that something is an element of aVectorSpaceobject. Strictly speaking this means thatWavefunctionobjects are vectors or basis functions an not everything derived fromWavefunctionwill strictly be a wavefunction. However, we felt the more apt names,VectororBasisFunction, were respectively too likely to collide with other libraries (including the standard library) or be misconstrued as AO-specific.ImplicitVector. Code factorization for representing a wavefunction belongs to anImplicitSpaceobject.Determinant. A class representing a wavefunction formed by taking determinants of single-product wavefunctions.
Other potential classes could include strong types for specific implicit vectors
(e.g., an Alpha class), explicit vectors that we don’t immediately need
individual tensor elements of at the moment (e.g., AO class), or other
multi-particle wavefunctions (e.g., RODeterminant or configuration state
function).
Operations
To make the objects in the wavefunction component behave like their real
life counterparts, we create an operations subcomponent that allows us to
describe the mathematical relationships between vector spaces. All of these
classes derive from VectorSpace.
Product. Indicates that the resulting vector space is obtained by taking the tensor product of a series of vector spaces.Transformed. Indicates that the vector space \(V\) is obtained from a (usually) different vector space \(V'\) via a linear transformation.Natural. Indicates that the vector space is spanned by the eigen vectors of a matrix.Naturalessentially pairs a vector space with eigen values of a matrix.Antisymmetrized. Takes the tensor product of \(n\) copies of a vector space \(V\) and antisymmetrizes the result, i.e., it creates the space spanned by determinants formed from \(n\) orbitals.
Other future operations could involve taking the union of vector spaces or symmetrized products (i.e., the space spanned by permanents).
One-Particle Derived Spaces
Classes in this subcomponent are obtained by applying operations to classes in the fundamental spaces subcomponent or to other one-particle dervied spaces.
MOs. A strong type to signal that aTransformed<AOs>object is being used as molecular orbitals.
SAOs. A strong type to signal that aProduct<AOs,Spin>object is being used as spin atomic orbitals (admittedly this does not seem to be a common concept, but its a natural basis for spinors and more familiar molecular spin orbitals).SOs. A strong type signalling that aTransformed<SAOSpace>is a set of (molecular) spin orbitals.CMOs. A strong type signalling that the molecular orbitals diagonalize the Fock matrix.CSOs. A strong type signalling that the spin orbitals diagonalize the Fock matrix.
At conception this component is seen as largely involving a series of strong
types. The strong types are important for two reasons: to simplify the types
that appear in compiler errors etc. and to distinguish between, say, MOs
that diagonalize the Fock matrix vs. MOs that diagonalize the density
matrix.
Many-Particle Derived Spaces
Classes in this subcomponent are formed by taking products of one-particle
vector spaces or by transforming other many-particle vector spaces. At present
we do not use strong types for members because CMOs / CSOs are uniquely
defined orbital spaces and thus the resulting \(n\)-particle spaces is
also uniquely defined
Note
AFAIK, there is no concise name for the various resulting spaces — e.g., I am unaware of a name for the \(n\)-fermion Hilbert space whose basis set is antisymmetrized tensor products of CMOs. The lack of such names is likely because the evaluation of the resulting equations only uses properties of the one-particle basis and thus it is far more important to be able to have terminology to distinguish among one-particle bases than many-particle bases.
Summary
- orbitals
The wavefunction component contains classes for expressing atomic orbitals (usually the most fundamental set of orbitals) as well as the myriad of orbitals that can be derived from them.
- determinants and permanents
Addressed by the
AntisymmetrizeandSymmetrizeclasses.- basis function vs basis set
Addressed with the
WavefunctionandVectorSpaceclasses, where the former is an element of the latter.- implicit vs explicit
The
ImplicitSpaceandImplicitVectorclasses are introduced to respectively implement basis sets and basis functions that are typically only distinguished from one another by names (e.g., “x” and “y” axes).- method dispatching
The use of strong types allows tensor elements to have different types depending on the wavefunctions the user provides. This in turn facilitates dispatching based on function overloading.
- bra/ket state
Addressed by having the various classes in the wavefunction component possess state.