Understanding Nested Tensors

Mathematically tensors can be very confusing objects because of the many isomorphisms that exist among them. While mathematics may be fine treating isomorphic structures as equivalent, most tensor libraries are not. By introducing the concept of a nested tensor we are better able to distinguish among mathematical ambiguities which arise because of the isomorphic nature of the structures.

Background

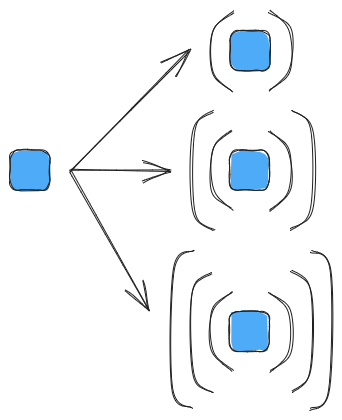
Fig. 2 Illustration of a scalar (the blue square), can equivalently be thought of as a vector, a matrix, and a rank 3 tensor.

Consider a tensor \(A\) with a single element in it. \(A\) is arguably best represented as a scalar (rank 0 tensor); however, if we wanted to, we could also represent \(A\) as a single element vector (rank 1 tensor), or a single element matrix (rank 2 tensor), or a single element rank 3 tensor, etc. This scenario is shown pictorially in Fig. 2.

Because these representations are related by an isomorphism, math says that all of these representations of \(A\) behave similarly. For better or worse, most tensor libraries are rather pedantic about representation, e.g., if \(A\) is declared as a vector, the user will need to provide one offset to access the single element. By requiring users to declare the rank of a tensor before use, the tensor library is able to avoid ambiguity and know how many indices to expect.

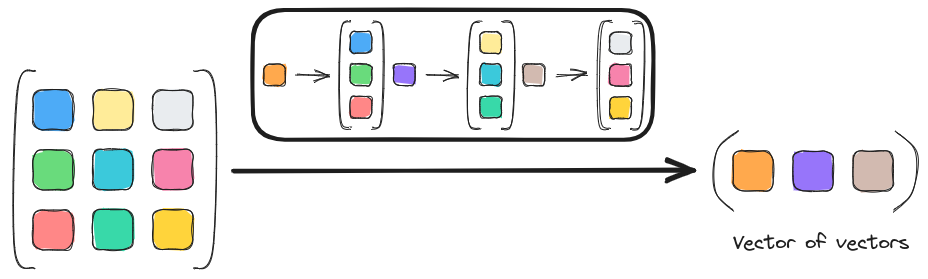
Fig. 3 While it is conventional to view a rank 2 tensor as having rank 0 elements, one can equivalently view it as having rank 1 elements, i.e. a vector of vectors.

Unfortunately, rank alone is not sufficient to remove all of the ambiguity. Another point of ambiguity comes from the fact that vectors, matrices, etc. are actually isomorphic with scalars. Fig. 3 summarizes this isomorphism of tensors, namely given that \(A\) has a rank \(r\) we can actually view the elements as having any rank between 0 ane \(r\) inclusive. When we choose to view the elements of \(A\) as having a rank greater than 0, we say that \(A\) is a nested tensor. Finally, note that it is possible for a rank \(r\) tensor to have up to \(r\) layers of nesting, which is to say that nesting is not limited to a tensor of tensors, but can also include tensors of tensors of tensors, etc.

Motivation

So why does the ambiguity from nesting matter? The short answer is performance. In TensorWrapper, the nesting of the physical layout (see Logical versus physical for the distinction between the logical and physical layouts) is used to determine how a tensor is physically stored. If the physical layout of the tensor has no nesting then TensorWrapper can store the tensor however it wants. If the physical layout has a nesting like that shown above in Fig. 3, then TensorWrapper will prioritize keeping columns of the matrix together. If instead the physical layout of a matrix is actually a rank 4 tensor resulting from tiling, like that shown on the right side of Fig. 1, then TensorWrapper knows to prioritize keeping slices together. Viewing the same tiled tensor as a matrix of vectors of vectors (a triply nested tensor) would tell TensorWrapper to first prioritize keeping the slices together and then second prioritize keeping either the rows or the columns of the slices together (whether the second priority is the rows or the columns depends on how the innermost vectors were defined).

Nested shapes were primarily developed to tell different physical layouts apart; however, there are some circumstances where the user may want to declare the logical layout to be nested. Ultimately nesting is a way of recursively partitioning a tensor. So if the problem the user is modeling is usually expressed in terms of equations which rely on partitioned tensors, then the user may opt to express the logical layout of the tensor as being nested. As an example, in many physics applications partitioned equations result from forces, energies, etc. that contain several identifiable components.

Summary

There are many different representations of the same tensor. While the results of formal tensor algebra are indifferent to the representation, numerical performance may change. To distinguish among the various ways of partitioning a tensor we introduce the concept of a nested tensor.