Designing TensorWrapper Class

The point of this page is to document the design process of the TensorWrapper class. Since TensorWrapper is the namesake class of the TensorWrapper project, and since the project and the class are two distinct entities, we establish the convention that when referring to the class we will use TensorWrapper whereas TensorWrapper denotes the project. This convention is used throughout the documentation not just on this page.

What is the TensorWrapper class?

The TensorWrapper class is TensorWrapper’s tensor class. Assuming most users of TensorWrapper are using TensorWrapper for tensor algebra, we anticipate that the bulk of user interactions with TensorWrapper will be through the TensorWrapper class (and technically the expression layer).

Why do we need the TensorWrapper class?

As an object-oriented tensor library, it is perhaps no surprise that TensorWrapper needs an object to represent a tensor. It is also worth noting that we have opted for the class to be named TensorWrapper instead of say Tensor owning to the fact that almost all of the potential backends will have a class named Tensor (or some variation on it).

TensorWrapper Considerations

Data storage

TensorWrapper objects ultimately hold all of the tensor’s state in some form or another.

Logical versus physical

As discussed in Logical Versus Physical: Understanding the Tensor Layout, we have a need for distinguishing between the logical layout of a tensor (how the user thinks of it) and the physical layout of the tensor (how it’s actually stored on the computer). These two, sometimes competing layouts come to a head in the TensorWrapper class. It is the responsibility of the TensorWrapper to distinguish between the two layouts and convert as necessary.

DSL entry point

In accordance with Einstein summation convention, users label the modes of a tensor to describe what they want to compute. This process effectively kicks off the creation of the concrete syntax tree (CST) which is at the heart of implementing the domain specific language (DSL).

Special tensors

When composing tensor expressions we sometimes need tensors like the identity tensor or the zero tensor. These tensors formally appear in equations usually as a mechanism for performing some other operation such as increasing the rank of a tensor or turning off a term. Actually creating, instantiating, and computing operations involving these “special” tensors would, in most cases, be detrimental to performance.

• We can rely on strong-typing of identity/zero tensors to identify them in the expressions.

• Private inheritance from TensorWrapper would prohibit users from implicitly converting them to TensorWrapper objects by mistake (at which point the strong-typing would be lost and we would have to evaluate them as full tensors).

• A member function wrapping the upcast to the base would allow the base to be publicly accessible, if explicitly wanted.

TensorWrapper Design

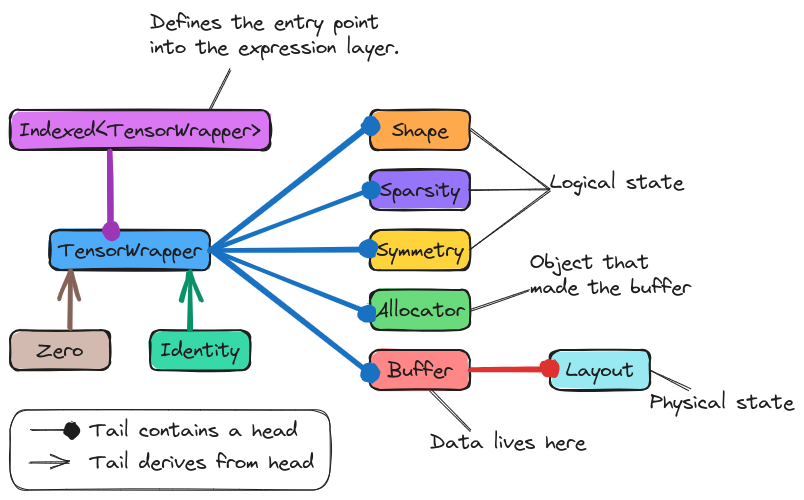
Fig. 13 Illustration of a TensorWrapper object’s state.

As Fig. 13 illustrates, the state of a TensorWrapper object is spread out over a number of objects. The Data storage consideration is ultimately satisfied by TensorWrapper objects containing a Buffer object. The Buffer object, specifically the Layout object underlying it, accounts for the “physical” portion of the Logical versus physical consideration. The “logical” portion of Logical versus physical is addressed by TensorWrapper also containing a Shape, Sparsity, and Symmetry object. Finally, the TensorWrapper class can be composed by creating Indexed<TensorWrapper> objects, satisfying the DSL entry point consideration.

To address Special tensors we derive from TensorWrapper two classes, Zero and Identity. Respectively these classes are intended to be strong types representing a zero tensor and an identity tensor. If needed, additional special tensors (such as the tensor representing a particular Levi-Civita symbol) could be added in an analogous manner.

Proposed APIs

Constructing TensorWrapper Objects

Particularly for tutorials and unit testing we often want to create objects quickly. To this end we propose an initializer list constructor which operates like:

// Makes a scalar
TensorWrapper s(1);

// Makes a 3 element vector with elements 1, 2, 3
TensorWrapper v({1, 2, 3});

// Makes a 1 element vector with element 1
TensorWrapper v1({1});

// Makes a 3 by 4 matrix
TensorWrapper m({{1, 2, 3, 4}, {5, 6, 7, 8}, {9, 10, 11, 12}});

// A jagged matrix where rows 0, 1, and 2 respectively have 2, 3, and
// 4 elements each
TensorWrapper jm({{1, 2}, {3, 4, 5}, {6, 7, 8, 9}});

The generalization to rank 3 tensors and other jagged tensors should hopefully be clear (we do not forsee initializing nested tensors with initializer lists to be a prominent use case; nested tensors can be created with the more general API, vide infra). In practice, the above calls actually:

• Create Shape, Sparsity, and Symmetry objects.

• Initialize a Layout from the Shape, Sparsity, and Symmetry objects.

• Declare a default Allocator object.

• Use the Allocator to create and initialize a Buffer object.

Thus the most general constructor for a TensorWrapper is:

// Note: that the actual constructors have overloads for cv-qualifiers,
// pointer vs reference semantics, etc.
TensorWrapper(Shape shape, Symmetry symmetry, Sparsity sparsity,
              AllocatorBase allocator, Buffer buffer);

Where the first three arguments define the logical layout of the tensor, buffer is the buffer containing the data, and allocator is the allocator which actually made buffer. In the early stages of development we suspect that actually creating a tensor will look like:

// Get runtime and logical layout
auto rv                          = get_runtime_view();
auto [shape, symmetry, sparsity] = get_logical_layout();

// Generate physical layout
auto layout = compute_layout(rv, shape, symmetry, sparsity);

// Choose an allocator compatible with the physical layout
auto allocator = choose_allocator(rv);

// Use the allocator and a lambda to fill in the buffer
auto buffer = allocator.construct(layout, [](){...});

// Create the TensorWrapper object
TensorWrapper t(shape, symmetry, sparsity, allocator, buffer);

Where the opaque functions get_runtime_view and get_logical_layout respectively wrap the process of getting a handle to the runtime (managed by ParallelZone) and defining the problem-specific aspects of the tensor. The remaining two opaque functions, compute_layout and choose_allocator will, for the early stages of TensorWrapper development, wrap the user manually creating the layout and selecting an allocator. The end goal of tensor wrapper is to automate these two steps and ideally construction of a TensorWrapper object will actually look like:

// Get runtime and logical layout
auto rv                          = get_runtime_view();
auto [shape, symmetry, sparsity] = get_logical_layout();

// Create a TensorWrapper object which has symmetry and sparsity
TensorWrapper t(shape, symmetry, sparsity, rv, [](){...});

// or create a TensorWrapper object which has no symmetry and is dense
TensorWrapper t2(shape, rv, [](){...});

We note that the actual signatures of the lambda function are dictated by the allocator component (see Proposed APIs for more information).

Composing TensorWrapper Objects

We anticipate that after construction, the next most common interaction with TensorWrapper objects will be composing them. Composition, for the most part, will rely on generalized Einstein summation convention:

// Assume that a and b are rank 3 tensors and extents of all operations below
// work out
auto [a, b] = get_initialized_tensor_wrapper_objects();

// Assignment is usually done into a default-initialized object
TensorWrapper c;

// Tensor addition:
c("i,j,k") = a("i,j,k") + b("j,i,k");

// Tensor subtraction with summation over k:
c("i,j") = a("i,j,k") - b("j,i,k");

// Scaled, element-wise multiplication
c("i,j,k") = 3.14 * a("i,j,k") * b("i,j,k");

// Tensor contraction over k
c("i,j") = a("i,j,k") * b("j,i,k");

// Element-wise division
c("i,j,k") = a("i,j,k") / b("i,j,k");

// Once a tensor has a state, can accumulate into it, e.g.,
c("i,j,k") += a("i,j,k");

Not all tensor algebra is expressed nicely using generalized Einstein summation convention, e.g., finding eigenvalues/eigenvectors. Since many of the backends have their own mechanisms for performantly carrying out such operations it is important that TensorWrapper wrap those mechanisms too. That said, while the above code snippet is designed to look like the operations are part of the TensorWrapper class, they are actually done by the expression component. More information on the design of the expression component, including how it extends to other tensor algebra needs is described in Designing the Expression Component.

TensorWrapper Summary

Data storage

This consideration is addressed by having the TensorWrapper class contain a Buffer object.

Logical versus physical

The Buffer object contains the physical layout of the tensor. The logical layout is spread across the Shape, Symmetry, and Sparsity objects which reside inside the TensorWrapper class.

DSL entry point

Annotating a TensorWrapper object with indices creates an Indexed<TensorWrapper> object. The Indexed<TensorWrapper> object is part of the expression layer which defines the DSL.

Special tensors

Zero and Identity classes are added which derive from TensorWrapper. Since these special tensors are represented by separate classes, the expression layer can use template meta-programming to optimize them out.