Designing the Expression Component
This page documents the process of designing the expression component of TensorWrapper.
What is the expression component?
Users of a tensor library have two main needs: to create tensors and to solve tensor expressions involving those tensors. The expression component contains the pieces of the domain specific language (DSL) required to write succinct tensor expressions.
Why do we need an expression component?
Most libraries tend to be eagerly evaluated, meaning code is evaluated as it is encountered. For simple, easily optimized code such a strategy is fine. Unfortunately, tensor expressions tend to be significantly harder to optimize, plus the optimal evaluation tends to be highly runtime dependent. A potential solution to this problem is to evaluate the code lazily, instead of eagerly. Lazily evaluated code is “recorded” until it is needed. Once it is needed it is played back.
Most tensor operations are steps in a bigger algorithm. By lazily evaluating tensor computations we can register the user’s intention and optimize our evaluation strategy accordingly. The point of the expression layer is to provide a user-friendly DSL for lazy evaluation of tensors.
Expression Component Considerations
- compose multiple objects
While our goal is to ultimately be able to compose
TensorWrapperobjects, we can decompose the work needed to do so by ensuring we can compose the pieces of theTensorWrapperobject. In particular we want to be able to compose objects from the shape, symmetry, sparsity, and allocator components.
- generalized Einstein notation
Many of the most common tensor operations are succinctly specified using generalized Einstein notation (indices appearing on the right side of an equation, but not the left are summed over).
There are some gotchas (see Einstein Summation Convention).
Math operations include: addition, subtraction, scaling, multiplication, and division. The latter is missing from a number of existing tensor libraries.
Note that multiplication actually covers a number of operations including: element-wise product, matrix multiplication, contraction, trace, and direct product.
Could actually enable an alternative syntax with explicit summations.
- non-Einstein math
There are a number of tensor operations which are not easily expressed using generalized Einstein notation, but are still important for tensor algebra. In particular:
Eigen system and linear equation solvers.
Factorizations/decompositions: Cholesky, QR, SVD.
Slicing/chipping
Matrix powers
- template meta-programming cost
In C++ lazy evaluation is typically implemented by using the template meta- programming technique known as expression templates. Ultimately expression templates map different expressions to different types. The type of an expression is usually a heavily nested instantiation of a template class, which can lead to significant compiler overhead (as well as nearly undecipherable compiler errors, though C++20 concepts helps a lot in this regard).
- reusable intermediates
In most tensor libraries the expression layer goes from a series of sources to a single sink. Along the way a series of temporary, unnamed intermediates is created. If any of these intermediates is common to more than one expression we want to make sure those intermediates are only formed once.
N.b. while an expression like
A("i,j,k") + B("i,j,k")is clearly an intermediate, so isA("i,j,k"). This is becauseA("i,j,k")corresponds to tensor access of the “i,j,k”-th element and may be non-trivial (also note that behind the scenes, for performance, TensorWrapper may map the element access to “slice access followed by element access”).
- sparse maps
The sparsity component Tensor Sparsity Design realized that sparse maps are a mechanism for creating sparsity objects and thus should live above the sparsity component. Sparse maps are most naturally expressed as relationships among dummy indices, that is given an expression like
C("i,j") = A("i,j,a,b") * B("i,j,b,a");we would define a sparse map, say which maps a giveni,jpair to a set of corresponding, non-zeroa,bpairs. From that sparse map we can work out the sparsity ofA,B, andC. The trick is we need to know how the sparse map’s modes map to the modes ofA,B, andC. This information is available in the expression layer.The design of the sparse map objects is punted to the sparse map component of TensorWrapper (see Designing the Sparse Map Component).
The API needs to work for sparse maps which map from one or more modes to one or more modes, i.e., we should not assume that we are always mapping a single mode to a single mode.
- linked
Ultimately all expressions which are to be treated together will need to be linked so they can share information. Linked in this context means that they share common state.
The lifetime of the common state will likely need to be managed by a shared pointer.
Out of Scope
- expression optimization
The goal of the expression layer is simply to capture the information needed to perform the calculation, not to optimize the calculation, or to perform it. Optimizing the calculation can be done using the OpGraph component (see Designing the OpGraph). Running the calculation is done by the backend of the Buffer component, given an OpGraph object (see Designing the Buffer).
- finding common intermediates
While consideration reusable intermediates concerns the expression layer being able to annotate common intermediates, actually finding said common intermediates is much harder. For now it is the user’s job to identify common intermediates.
- filling in the sparse maps
Sparse maps are an alternative means of specifying sparsity. As with the objects in the sparsity component (see Tensor Sparsity Design) filling in the sparse map is left to the user.
Expression Component Design
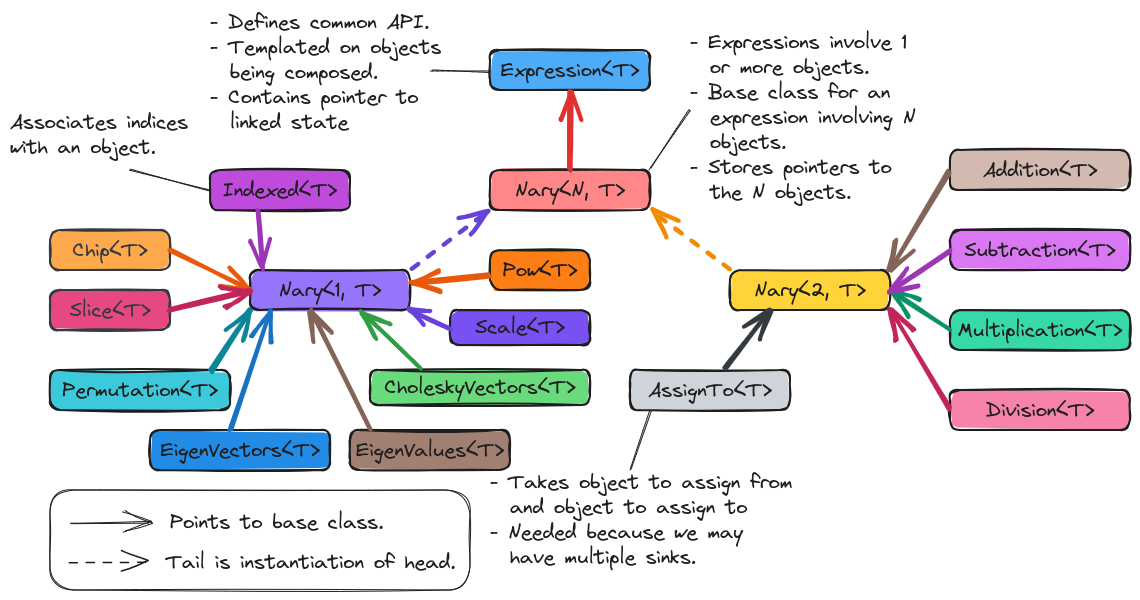
Fig. 14 Overall inheritance diagram for the classes comprising the expression component of TensorWrapper.
Fig. 14 shows the classes involved in TensorWrapper’s expression component and how they are related. The following subsections describe the main highlights of the hierarchy in more detail.
Expression
The base of the class hierarchy
is Expression<T> which is templated on the type of object being composed.
For example viable options for T are Shape and TensorWrapper.
Templating on the object being composed addresses
compose multiple objects. The Expression<T> object will also
contain a pointer to the linked state (see consideration linked).
The main motivation for this class is to define the API all derived classes must obey and then to interact with those classes through the base class. In particular this approach relies on dynamic polymorphism, not the static polymorphism usually leveraged in expression templates. This paves the way for addressing template meta-programming cost.
As a note, since the API for composing expression objects will involve taking objects by their base class and returning them wrapped in a derived class, to avoid loops in the hierarchy where the base class depends on the derived class, most operations will need to be defined as free functions. For example:
Addition<T> operator+(const Expression<T>& lhs, const Expression<T>& rhs);
CholeskyVectors<T> cholesky(const Expression<T>& A);
The definitions will
One of the key properties of any Expression<T> object is that when assigned
to an object of type Indexed<T> it can produce an object of type T.
Note
Because assigning to Indexed<T> has to be treated specially care needs
to be taken in defining copy/move assignment operators.
Nary
Deriving from Expression<T> is the Nary<N,T> class (n-ary being the
generalization of unary, binary, trinary, etc. to n objects). This class serves
as code-factorization for objects which must hold pointers/references to N
objects of type T. We have opted to specify N statically since it is
almost always known ahead of time. While N==1 and N==2 scenarios are
most common, we can envision optimizations which may be enabled by having
higher values of N (for example triple products).
Unary
Most of the tensor algebra falling under the non-Einstein math consideration involves operations on a single object.
For taking slices/chips of the object we respectively have the
Slice<T>/Chip<T>classes.Permuation<T>represents permutations of the modes.EigenVectors<T>andEigenValues<T>respectively represent the eigenvectors and eigenvalues resulting from an eigen decomposition.Similarly,
CholeskyVectors<T>represents the Cholesky vectors resulting from a Cholesky decomposition.Scale<T>scales anExpression<T>by a constant.Pow<T>represents taking a matrix power (could template on the power too since I think it’s usually known at compile time also).
The last unary class is Indexed<T> which is a bit of a special class. Given
a series of objects of type T, the objects are promoted to the
expression layer by annotating the modes (providing string labels). The object
which results from annotating the modes is an instance of Indexed<T>. The
reason this class is special is that the only way to get back to objects of type
T, i.e., to leave the expression layer is by assigning an
Expression<T> object to an Indexed<T> object.
Binary
Members of the binary series of classes involve combining two objects. Most tensor algebra which can be expressed using generalized Einstein summation convention (consideration generalized Einstein notation) falls under this category.
Addition<T>results from adding twoExpression<T>objects together.Subtraction<T>results from subtracting twoExpression<T>objects.Multiplication<T>results from multiplying twoExpression<T>objectsDivision<T>results from dividing twoExpression<T>objectsAssignTo<T>results from assigning anExpression<T>to anIndexed<T>object. These objects are only ever created for generating nodes of the abstract syntax tree (AST).
User API
This section focuses on what the user actually writes. The next section looks at how the DSL works in more detail, by filling in the blanks regarding the many unnamed temporary objects these code snippets hide.
Construction
Most tensor operations will look like tensor math written using the generalized Einstein summation convention. Some examples:
auto [a, b] = fill_in_a_and_b();
T c, d, e, g; // No "f" to make connection to the example API section
c("i,j,k") = a("i,j,k") + b("i,j,k");
d("i,j,k") = a("i,j,k") * b("i,j,k");
e("i,j,k") = a("i,j,k") - b("i,j,k");
g("i,j,k") = a("i,j,k") / b("i,j,k");
Since these lines all involve unnamed temporary intermediates, each line must
be treated as a separate expression, i.e., there is no way to preserve the
lifetime of the intermediates from one line to another. Hence, in order to
satisfy reusable intermediates, we require that the user assigns at
least one of the common intermediates (recall an intermediate is as simple as
a("i,j,k")) to a named variable, e.g.:
{
auto aijk = a("i,j,k");
c("i,j,k") = aijk * b("i,j,k");
d("i,j,k") = aijk / b("i,j,k");
}
In practice the way this will work is that the Buffer objects actually
assigned to c and d are FutureBuffer objects (see
Designing the Buffer). The FutureBuffer objects will be tied to
the lifetime of the expression layer which generated them. When all expression-
layer objects involved in creating the FutureBuffer objects go out of scope
evaluation begins. So if we want to ensure that the above two equations are
treated as a set of equations, and not two individual equations, we need to make
sure at least one of the expression-layer objects is present in each equation
(the {} are needed to establish a scope for aijk, ensuring it goes out
scope after the second equation).
While it is theoretically possible for TensorWrapper to correctly identify the
two temporary objects in the previous code block that result from b("i,j,k")
as identical, it is unlikely that TensorWrapper will contain such optimizations
in the near future. Hence best practice will be to assign each common
intermediate to a named variable, i.e., the above code block should really be
written as:
{
auto aijk = a("i,j,k");
auto bijk = b("i,j,k");
c("i,j,k") = aijk * bijk;
d("i,j,k") = aijk / bijk;
}
so that the expression layer will identify b("i,j,k") as evaluating to the
same intermediate.
Non-Einstein Algebra
In order to perform operations which involve tensor algebra that can not be expressed using generalized Einstein summation convention, we still require the user to annotate the modes of the tensor (this is so we can generate and track an CST). Proposed user APIs are:
T L, Lt, v, λ, a10_10, a2;
{
auto Aij = A("i,j");
// disclaimer, I'm not 100% sure the cholesky/eigen_solve APIs will work
// as shown, but it should be possible to get something close.
// A = LLt
L("i,j") = cholesky(Aij);
// Av = λBv (no argument needed if B is 1)
std::make_pair(v("i,j"), λ("j")] = eigen_solve(Aij, B("i,j"));
// Get the slice of A starting a 0,0 and extending to 10,10 exclusive.
a10_10("i,j") = slice(Aij, {0, 0}, {10, 10});
// Raise A to the power 2
a2("i,j") = pow(Aij, 2);
}
The above code actually would create one set of expressions since Aij is
used in all of the expressions.
Sparse Maps
Each element of a particular set of expressions will necessarily have access to the same graph. The user should thus be able to set the sparse maps through any element of the expression layer, e.g.,
{
auto Lij = get_sparse_map_from_mode_i_to_mode_j();
auto Lik + get_sparse_map_from_mode_i_to_mode_k();
auto aijk = a("i,j,k");
auto bijk = b("i,j,k");
c("i,j,k") = aijk * bijk;
d("i,j,k") = aijk / bijk;
aijk.set_sparse_map("i", "j", Lij);
aijk.set_sparse_map("i", "k", Lik);
}
The above registers two sparse maps: one which for a given offset along modes
labeled with "i" gives non-zero offsets along modes labeled with j" and
a similar sparse map for modes labeled with "i" to modes labeled with
"k". Note that for this API to work the user MUST use indices consistently,
which is to say i", "j", and "k" must be indexing the same modes
each time they appear.
Example API
Note
The examples in this section purposely use the real types from the expression layer. This is NOT what we expect a user to do. What a user sees is shown later (see User API).
The expression layer works basically the same for every composable object of
type T (T being things like Shape, Symmetry, TensorWrapper)
so we avoid specifying the value of T. The APIs shown in this section are
more to flesh out how the unnamed temporaries actually interact.
Construction
Following from the generalized Einstein notation consideration we expect that most users will enter into the expression layer by adding dummy indices to an object. This looks like:
// Assume we have some T objects
T a, b, c, d, e, g; // No f b/c variable would be "if"
Indexed<T> ia = a("i,j,k");
Indexed<T> ib = b("i,j,k");
Indexed<T> ic = c("i,j,k");
Indexed<T> id = d("i,j,k");
Indexed<T> ie = e("i,j,k");
Indexed<T> ig = g("i,j,k");
The Indexed<T> objects will then be composed pair-wise to form
BinaryExpression<T> objects.
// continues from last code block
Addition<T> iapib = ia + ib;
Multiplication<T> iatib = ia * ib;
Subtraction<T> iasib = ia - ib;
Division<T> iadib = ia / ib;
Note that unlike traditional expression templates which would end up with
types like Addition<Indexed<T>, Indexed<T>> we rely on the fact
the all of the pieces derive from Expression<T>, which helps us address
consideration template meta-programming cost.
Once we have built up terms they get assigned to an Indexed<T> object like:
// continues from last two code blocks
ic = iapib; // Assigns results of addition to C
id = iatib; // Assigns results of multiplication to C
ie = iasib; // Assigns results of subtraction to C
ig = iadib; // Assigns results of division to C
It is worth noting, that it is somewhat trivial to satisfy consideration reusable intermediates when interacting with the expression layer directly. This is because each expression object is actually a node in the concrete syntax tree (CST), so by reusing the literal nodes we reuse the intermediates.
From this we can see that c("i,j") = a("i,j") + b("i,j"); actually works
by:
a("i,j,k")creates an unnamed temporaryIndexed<T>object,b("i,j,k")creates another unnamed temporaryIndexed<T>object,the
Indexed<T>::operator+method is then called on the previous two temporary objects resulting in a third temporary of typeAddition<T>c("i,j,k")creates yet another temporaryIndexed<T>object.Finally
Indexed<T>::operator=is called assigning theAddition<T>object to the the temporary resulting fromc("i,j,k").
Non-Einstein Algebra
The previous section showed how to write tensor algebra for operations which can be expressed using generalized Einstein summation convention. Consideration non-Einstein math means that the expression layer must be able to support other tensor algebra operations as well. In terms of expression-layer objects:
auto [A, B] = get_filled_matrices();
T L, Lt, v, λ, a10_10, a2;
// A = LLt
CholeskyVectors<T> L = cholesky(Aij);
// Av = λBv (argument only needed for generalized eigen_solves)
std::pair<EigenVectors<T>, EigenValues<T>> vλ = Aij.eigen_solve(Bij);
// Get the slice of A starting a 0,0 and extending to 10,10 exclusive.
Slice<T> a10_10 = slice(Aij, {0, 0}, {10, 10});
// Raise A to the power 2
Pow<T> a2 = pow(Aij, 2);
The trick to satisfying non-Einstein math consideration is that we
require the various operations to involve tensors which are already wrapped in
expression-layer constructs. While this is a bit more verbose, it also allows
us to, in some cases (like the slice operation), support transposing the
result.
Obtaining an OpGraph
The trick to avoid the nasty nested expression templates is to obtain the final
OpGraph object via the base class’s Expression<T> API. This can be
done via the visitor pattern and looks something like:
// In practice e would be a pointer b/c Expression is an abstract base class
Expression<Shape> e = get_expression();
auto [graph, node] = e.add_to_graph(OpGraph{});
Then internally the add_to_graph method of the most derived class,
Derived<T>, is implemented something like:
std::pair<OpGraph, Node> Derived<T>::add_to_graph(OpGraph g){
// Assume Derived<T> inherits from Base<T>
auto [subgraph, parent_node] = Base<T>::add_to_graph(g);
// Create node corresponding to Derived<T> add to parent_node
// Return new graph and new node
}
This works because Expression<T> defines a virtual function
std::pair<OpGraph, Node> add_to_graph(OpGraph g) which is overridden by each
of the derived classes. Each derived class calls the base class’s
add_to_graph method, which in turn returns the graph and the node just
added. Exactly what the nodes look like, and what information they contain is
punted to the OpGraph component (see Designing the OpGraph).
Understanding the Linked State
Pursuant to the linked consideration, expression component objects belong to the same set of expressions must share a common state. The purpose of this section will be to work out the lifetime semantics and shared behavior of this state.
TODO: We can punt on this until we’re ready to implement it.
Summary
The above design satisfies the considerations raised in Expression Component Considerations by:
- compose multiple objects
The entire expression layer is templated on the type of the object being composed. This allows the expression layer to be reused with various pieces of the
TensorWrapperclass (e.g., theShapeclass) in addition to theTensorWrapperclass itself.- generalized Einstein notation
The entry pont to the expression layer is, for most operations, is assigning indices to a tensor’s modes. The resulting objects can then be composed using generalized Einstein notation.
- non-Einstein math
Tensor operations which can not be expressed using generalized Einstein summation convention are supported, but in order to ensure they interact with the expression layer we still require the tensors to have their modes annotated.
- template meta-programming cost
Instead of templating the various pieces of the expression layer on the types of the sub-expressions, as is usually done, we only template the expression layer pieces on the types of the object being composed, e.g., the template type parameter would be something like
ShapeorTensorWrapperinstead of say a type likeAddition<Indexed<Shape>, Indexed<Shape>>.- reusable intermediates
Each object in the expression layer is a node of a CST. Reusing the same object in multiple places reuses the same node of the CST.
- sparse maps
The objects associated with a particular set of expressions are linked. Using any of these objects the user can set one or more sparse maps which will then work out the sparsity for the set of equations.
- linked
The linked state of the expression component is described in the Understanding the Linked State section.
Other Notes
At some point we’ll probably need a way of applying arbitrary functions to
slices of one or more tensor. Such an operation could conceivably be built into
the Nary<N,T> class and the classes which derive from it