Tensor Shape Design

This page captures the design process of TensorWrapper’s Shape class.

What is a tensor’s shape?

For computing purposes, tensors are really nothing more than a bunch of floating point values and meta-data associated with those values. Conceptually, the floating point values are typically arranged into \(n\)-dimensional rectangular arrays, where \(n\) is the number of mode s in the tensor. A tensor’s shape describes this hyper-rectangular array’s layout.

Why do we need a tensor’s shape?

A tensor’s shape is arguably the most primitive meta-data associated with the tensor. Without the shape of the tensor we do not know how to access elements or lay them out in memory.

Shape Considerations

Basic operations

The unifying theme of objects in the shape component is that they describe the layout of the hyper-rectangular array of values. This means they need to represent:

rank
extent
sub-shapes (a sub-shape can be either a slice or a chip)
N.B., some, all, or none of these properties may be known at compile time and we need a mechanism for setting them at runtime.

Nested

While a nested tensor may seem exotic, in practice, distributed tensors are often implemented by nesting (ideally the user need not be aware of such nesting aside from possibly specifying it at construction). Nesting, also occurs naturally when discussing sparsity.

Nestings may be smooth or jagged.
While nestings can be flattened (e.g., a smooth matrix of matrices can just be treated as a rank 4 tensor and a smooth matrix of jagged matrices can be treated as a single jagged rank 4 tensor) doing so destroys the mode partitioning information.
Mode partitioning information is needed for providing hints to the backend pertaining to slicing operations and hierarchical memory layouts.

Jagged-ness

A truly jagged shape (one where slices along the same mode have different shapes) require special treatment.

Requires the tensor be at least rank 2 to be truly jagged.
Must have smooth slices of at least rank 1, but could have higher-rank smooth slices, e.g., a jagged rank 3 tensors could have smooth matrices as elements.
A jagged tensor of rank \(r\), which has smooth slices of rank \(s\) must minimally be viewed as having \(r-s\) layers
A key use of jagged shapes is for tiling tensors.
Another use of jagged shapes is for when you do not want to pad a mode (add zeros for unused basis functions). Put another way, in theory, a jagged shape can always be turned into a smooth shape by introducing padding; however, doing so may have performance complications if the number of padding elements is significant.

Combining shapes: As we do tensor operations we will need to work out the resulting shapes. This in general requires knowing how the modes of the inputs map to the modes of the output.

Iterable

A natural use case of a shape is to iterate over the indices in the shape.

For iterating, it is useful to be able to set the origin. This allows iterating over slices using the original tensor’s indices.
Sometimes we want the absolute indices (starting from the origin) and other times we only want the offsets (always relative to zero).

Not in Scope

Sparsity

The Shape component is targeted at describing the conceptual layout of the hyper-rectangular array of values. The conceptual layout is independent of the values of the elements. Sparsity is concerned with knowing which elements are zero.

Sparsity is punted to Tensor Sparsity Design.

Permutational Symmetry

In many cases the elements of a tensor are not all linearly-independent and optimizations are possible by avoiding redundant computation.

Antisymmetry, Hermitian, and anti-Hermitian all fall into this consideration too.
Symmetry is punted to Designing the Symmetry Component.

Logical vs physical

See Logical Versus Physical: Understanding the Tensor Layout for a full description, but the point is that the user may declare a tensor to have a shape different from how the tensor is actually stored.

Both the logical and actual shapes are Shape objects.
It is the responsibility of the user creating Shape objects to track if they represent logical or actual shapes.

Masks

Shapes are index contiguous. Masks allow you to view a non contiguous set of indices as if they were contiguous. Masks can be implemented on top of the shape component and are therefore not in scope for this discussion.

Memory allocation.

The shape simply describes the hyper-rectangular array of values, it does not allocate memory for those values. Allocating memory is the responsibility of the allocator component (see Designing the Allocator).

Shape Design

In designing the class hierarchy we note the following:

An algorithm which works for a jagged shape should work for a smooth shape as well. The reverse, smooth algorithms with jagged shapes, will in general not work.
Nestings are logically imposed over an existing shape. The resulting nested shape is still an instance of the underlying shape.
Tiled shapes are a subcategory of jagged shapes.

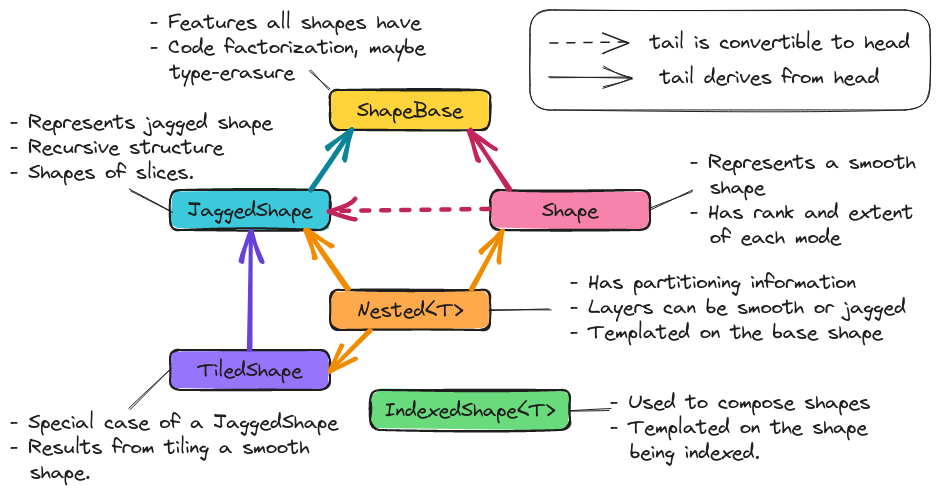
../../_images/shape.png — Fig. 6 The architecture of TensorWrapper’s Shape component.

Fig. 6 shows the classes primarily responsible for implementing the shape component. Most end users will deal with the Shape class.

ShapeBase

The unifying features of all shapes were summarized in the Basic operations consideration. ShapeBase provides the API that all shapes must minimally satisfy because they are shapes. The actual class serves primarily as code factorization.

Shape

The Shape class describes a (smooth) hyper-rectangular array of data and can be used for “traditional” tensors (those which are not nested or jagged). Most end users will simply create Shape objects and pass them on to TensorWrapper. We expect that manipulations of Shape objects will be aimed at TensorWrapper developers.

JaggedShape

To satisfy the Jagged-ness consideration we introduce JaggedShape. JaggedShape is similar to Shape except that users must explicitly provide the shape of the slices. Generally speaking JaggedShape objects of rank \(r\) will contain a series of rank \(s\) Shape objects. The actual JaggedShape object serves as a map from an index with \((r-s)\) indices to the Shape of that slice. Like Shape we expect users to primarily be concerned with construction. Again, manipulations of the JaggedShape will be primarily of interest to TensorWrapper developers.

TiledShape

Introduced primarily as a convenience for constructing JaggedShape objects by tiling.

Nested

To address the Nested consideration, we have added a Nested<T> class which is templated on the type of the tensor’s overall shape.

With objects like Shape and JaggedShape, TensorWrapper can’t tell how the user is thinking of the tensor. For example, they could be thinking of a matrix as a matrix or as a vector of vectors. The point of the Nested<T> object is to partition the ranks of the tensor into layers, so we know how many layers the user is viewing the tensor as, and how many ranks each layer has. Mathematically the various ways of a viewing a tensor do not change the properties of the tensor; however, when we are physically laying the tensor out on the computer, how we view the tensor can affect physical layout.

IndexedShape

Consideration Combining shapes requires us to be able to compose the various shape objects. To do this, we rely on the same mechanism used for TensorWrapper, i.e., an expression layer. More specifically, IndexedShape objects result from indexing a shape like s("i,j,k"). While IndexedShape is technically exposed to the user, user can be somewhat oblivious to its existence.

Proposed Shape APIs

Constructing a `Shape`

Creating a non-nested shape just requires knowing the extent of each mode:

Shape null_shape;              // No rank and no elements
Shape rank0_shape{};           // A scalar
Shape rank1_shape{10};         // 10 element vector
Shape rank2_shape{10, 20};     // 10 by 20 matrix
Shape rank3_shape{10, 20, 30}; // 10 by 20 by 30 tensor

Note that following usual C++ rules the first two lines actually call different constructors (default ctor vs. initializer list). Using an initializer list requires us to know the rank at compile time. If we want to determine the rank at runtime we can use iterators:

// Somehow create a vector of extents
using size_type = Shape::size_type;
std::vector<size_type> extents = get_extents();

// Construct Shape from iterator pair
Shape runtime_rank_shape(extents.begin(), extents.end());

Jagged Shape Construction

For a Shape we need to specify the extents of each mode. JaggedShape declaration is done in terms of Shape objects and looks like:

// For brevity define variables
Shape s10{10}, s20{20}, s30{30};
Shape s10_20{10, 20}, s30_40{30, 40}, s50_60{50, 60};
Shape s10_20_30{10, 20, 30}, s40_50_60{40, 50, 60};

// No elements, no rank
JaggedShape null_shape;

// Smooth scalar viewed as a JaggedShape (note () not {})
JaggedShape smooth0_shape(Shape{});

// Smooth vector viewed as a JaggedShape (note () not {})
JaggedShape smooth1_shape(Shape{10});

// Smooth matrix viewed as a JaggedShape (note () not {})
JaggedShape smooth2_shape(Shape{10, 20});

// A "jagged" vector with no elements
JaggedShape rank0_shape{};

// A jagged matrix with 1 row, note the {}
JaggedShape rank2_shape{s10};

// A jagged matrix with 3 rows; row 0 has 10 elements, row 1 has 20, row 2 30
JaggedShape rank2_shape2{s10, s20, s30};

// A jagged rank 3 tensor with smooth matrices. Matrix 0 is 10 by 20,
// matrix 1 is 30 by 40, and matrix 2 is 50 by 60
JaggedShape rank3_shape{s10_20, s30_40, s50_60};

// A jagged rank 3 tensor where elements are jagged matrices. Matrix 0 is
// 1 by 10, matrix 2 has 20 columns in row 0 and 30 columns in row 2, and
// matrix 3 has 30 columns in row 0, 10 columns in row 1, and 20 columns in
// row 2
JaggedShape rank3_shape2{{s10},
                         {s20, s30},
                         {s30, s10, s20}};

 // A jagged rank 4 tensor where the 0-th element of the 0-th mode is a
 // 10 by 20 by 30 smooth tensor and the 1-st element is a 40 by 50 by 60
 // smooth tensor
JaggedShape rank4_shape{s10_20_30, s40_50_60};

// A jagged rank 4 tensor where the elements are jagged rank 3 tensors.
// Taking slices along the 0 and 1-st modes, the (0,0)-th slice is a 10 by 20
// matrix, the (0,1)-th slice is a 30 by 40 matrix, the (1,0)-th slice is
// a 30 by 40 matrix, the (1,1)-th slice is a 10 by 20 matrix, and the
// (1,2)-th slice is a 50 by 60 matrix
JaggedShape rank4_shape2{{s10_20, s30_40},
                         {s30_40, s10_20, s50_60}};

// A jagged rank 4 tensors where the elements are jagged rank 3 tensors,
// which have jagged matrices for elements. Taking slices along the 0, 1, and
// 2 modes we have:
// - (0,0,0) is a 10 element vector,
// - (0,1,0) is a 20 element vector,
// - (0,1,1) is a 30 element vector,
// - (1,0,0) is a 10 element vector,
// - (1,0,1) is a 30 element vector,
// - (1,1,0) is a 20 element vector,
// - (1,2,0) is a 10 element vector,
// - (1,2,1) is a 20 element vector,
// - (1,2,2) is a 30 element vector
JaggedShape rank4_shape{{{s10}, {s20, s30}},
                        {{s10, s30}, {s20}, {s10, s20, s30}}};

Consider the shape of the (0,1) slice of rank4_shape. This slice is a vector of vectors where the outer vector has two elements, element 0 of the outer vector is a 10-element vector and element 1 is a 30-element vector. In other words the shape of the (0,1) slice of rank4_shape describes a jagged matrix, which could have been initialized by JaggedShape{s20, s30}. In turn the above construction of rank4_shape is actually equivalent to:

JaggedShape e00{s10};
JaggedShape e01{s20, s30};
JaggedShape e10{s10, s30};
JaggedShape e11{s20};
JaggedShape e12{s10, s20, s30};
JaggedShape e0{e00, e01};
JaggedShape e1{e10, e11, e12};
JaggedShape rank4_shape{e0, e1};

And we see that JaggedShape is a recursive structure and thus the runtime mechanism for initializing a JaggedShape is with iterators running over JaggedShape objects:

std::vector<JaggedShape> slice_shapes = get_slices();
JaggedShape shape(slice_shapes.begin(), slice_shapes.end());

So far we have focused on the most general way to create a JaggedShape one of the most common ways to form a JaggedShape is by tiling. Consider a 30 by 30 matrix where we tile each mode into 5, 15, and 10 element chunks. Using JaggedShape this can be done by:

JaggedShape js{{Shape{5,5}, Shape{5, 15}, Shape{5,10}},
               {Shape{15,5}, Shape{15,15}, Shape{15,10}},
               {Shape{10,5}, Shape{10,15}, Shape{10,10}}};

This is an admittedly verbose declaration. Thus for the special case of crating JaggedShape objects which result from tiling smooth Shape objects we introduce the TiledShape class. Using TiledShape the same shape could be declared via:

TiledShape s{{5, 10, 15}, {5, 10, 15}};

Constructing Nested Shapes

Creating a Nested<T> object requires knowing the shape of the tensor and how the indices are partitioned into layers.

// Zero layer scalar
Nested<Shape> s({}, Shape{});

// One layer scalar
Nested<Shape> s0({0}, Shape{});

// Two layer scalar
Nested<Shape> s0_0({0, 0}, Shape{});

// One layer vector
Nested<Shape> s1({1}, Shape{10});

// Two layer vector (mode in layer 0)
Nested<Shape> s1_0({1, 0}, Shape{10});

// Two layer vector (mode in layer 1)
Nested<Shape> s0_1({0, 1}, Shape{10});

// One layer matrix
Nested<Shape> s1({2}, Shape{10, 20});

// Two layer matrix (both modes in layer 0)
Nested<Shape> s2_0({2, 0}, Shape{10, 20});

// Two layer matrix (one mode per layer)
Nested<Shape> s1_1({1, 1}, Shape{10, 20});

// Two layer matrix (both modes in layer 1)
Nested<Shape> s0_2({0, 2}, Shape{10, 20});

// One layer rank 3
Nested<Shape> s3({3}, Shape{10, 20, 30});

// Two layer rank 3 one mode in layer 0 two in layer 1
Nested<Shape> s1_2({1, 2}, Shape{10, 20, 30});

// Three layer rank 3, one mode per layer
Nested<Shape> s1_1_1({1, 1, 1}, Shape{10, 20, 30});

// A two-layer shape where modes 0 and 1 are in layer 0 and modes 2 and 3
// are layer 1
Nested<Shape> s({2, 2}, Shape{5, 10, 15, 20});

The general syntax for an \(n\) layer tensor is an \(n\) element container where the \(i\)-th element is the number of ranks in that layer (ranks from the shape object are assigned to layers left to right; so permutations may be needed to line up with layering).

Basic Operations

All shapes know their total rank and the total number of scalar elements:

Shape s{10, 20, 30};
JaggedShape js{s, Shape{10, 20}};

// Total rank of the tensor
assert(s.rank() == 3);
assert(js.rank() == 3);

// Total number of elements in the tensor
assert(s.size() == 6000);  // 10 * 20 * 30 = 6000
assert(js.size() == 6200); // 6000 + (10*20) = 6200;

Nested additionally allows you to get this information per layer:

Nested<Shape> s1_2({1, 2}, s);
Nested<JaggedShape> js1_2({1, 2}, js);

assert(s1_2.n_layers() == 2);
assert(js1_2.n_layers() == 2);

assert(s1_2.rank_layer(0) == 1);
assert(s1_2.rank_layer(1) == 2);
assert(js1_2.rank_layer(0) == 1);
assert(js1_2.rank_layer(1) == 2);

assert(s1_2.elements_in_layer(0) == 10);
assert(s1_2.elements_in_layer(1) == 6000);
assert(js1_2.elements_in_layer(0) == 2);
assert(js1_2.elements_in_layer(1) == 6200);

// Get the shape of the 0,0-th element (returns a std::variant)
assert(s3_3({0, 0}) == s);

Shape Composition

Shape and JaggedShape objects are composed similarly (with JaggedShape objects having many more checks to ensure slices are of compatible sizes).

Shape s0{10, 20, 30}, s1;
JaggedShape js0{Shape{10}, Shape{20}}, js1;

// Since addition, subtraction, and element-wise multiplication only work out
// the shape of the result, they often amount to copying the state on the
// right side of the assignment operator (possibly with a permutation)
s1("i,j,k") =  s0("i,j,k") + s0("i,j,k");
assert(s1 == s0);

js1("i,j") = js0("i,j") + js0("i,j");
assert(js1 == js0);

// Permuting modes
s1("j,i,k") = s0("i,j,k") + s0("i,j,k");
assert(s1 == Shape{20,10,30});

js1("j,i") = js0("i,j") + js0("i,j");
assert(js1 == JaggedShape{Shape{20}, Shape{10}});

// Contraction
s1("i,k") = s0("i,j,k") * s0("i,j,k");
assert(s1 == Shape{10, 30});

// js0 is a jagged matrix with 2 rows, contracting over the variable number
// of columns gives a 2 by 2 matrix (represented as jagged matrix even though
// it's smooth)
js1("i,k") = js0("i,j") * js0("k,j");
assert(js1 == JaggedShape{Shape{2}, Shape{2}});

// These would throw since contracted modes aren't the same length
// s1("i,k") = s0("j,i,k") * s0("i,j,k");

// js1("i,k") = js0("i,j") * js0("j,k");

// Direct product
s1("i,j,k,l") = s0("i,j,k") * s0("i,j,l");
assert(s1 == Shape{10, 20, 30, 30});

js1("i,j,k") = js0("i,j") * js0("i,k");
assert(js1 == JaggedShape{Shape{10,10}, Shape{20,20}});

Combining Nested<T> objects is conceptually done layer-by-layer. In practice we just combine the underlying T objects while preserving the layer assignments and ensuring layer shapes are compatible:

Shape s{10, 20, 30};
Nested<Shape> s1_2({1, 2}, s), s2_1({2,1}, s), result;

result("i,j,k") = s1_2("i,j,k") + s1_2("i,j,k");
assert(result == s1_2);

// Not allowed because we can't add rank 1 tensors to rank 2 tensors
// result("i,j,k") = s1_2("i,j,k") + s2_1("i,j,k");

result("i,j") = s1_2("i,j,k") * s1_2("i,j,k");
assert(result == Nested<Shape>({1, 1}, Shape{10, 20}));

result("j,k") = s1_2("i,j,k") * s1_2("i,j,k");
assert(result == Nested<Shape>({0,2}, Shape{20, 30}));

// Layers only need compatible, not identical, shapes
result("j,k") = s1_2("i,j,k") * s2_1("i,j,k");
assert(result == Nested<Shape>({1, 1}, Shape{20, 30}));

We note that it’s quite likely that scenarios will arise where the user will want the result to be layered different than the default behavior provides. In practice re-layering a shape is a trivial operation (swapping two small vectors of integers).

Slicing and Chipping

Slices of a shape have the same rank, chips have different ranks:

Shape s{10, 20};

// Get the shape of row 0 as a matrix
auto s0 = s.slice(0);
assert(s0 == Shape{1, 20});

// Get the shape of column 0 as a matrix
auto sx0 = s.slice({0, 0}, {10, 1});
assert(sx0 == Shape{10, 1});

// Get the shape of the first five columns of the first five rows...
auto s05_05 = s.slice({0,0}, {5,5});
assert(s05_05 == Shape{5, 5});

// Note that this shape still refers to a rank 2 tensor even though the
// first mode has a single element
auto s01_05 = s.slice({0, 0}, {1, 5});
assert(s01_05 == Shape{1, 5});

// Get the shape of row 2 as a vector
auto s2 = s.chip(2);
assert(s2 == Shape{20});

// Get the shape of column 2 as a vector
auto sx2 = s.chip({0, 2}, {10, 3});
assert(sx2 == Shape{10});

For a rank \(r\) tensor, the general overload of slice and chip takes two \(r\)-element vectors. The first vector is the first element in the slice/chip and the second vector is the first element not in the slice/chip. For convenience we also provide an overload where the user may provide up to \(r\) integers. This overload pins the \(i\)-th mode to the \(i\)-th integer all other modes run their entire span.

Slicing and chipping JaggedShape objects is largely the same:

JaggedShape js0{Shape{10}, Shape{20}};

auto j0 = js0.chip(0);
assert(j0 == JaggedShape{Shape10});

auto j1 = js0.slice(0);
assert(j1 == JaggedShape({Shape{10}});

Because chipping selects a single element per mode per layer, chipping a Nested object is fairly straightforward:

Nested<Shape> s2_2({2, 2}, Shape{2, 2, 10, 10});
assert(s2_2.chip(0) == Nested<Shape>({1, 2}, Shape{2, 10, 10}));
assert(s2_2.chip(1,2) == Shape{10, 10});
assert(s2_2.chip(1,2,3) == Shape{10});e
assert(s2_2.chip(1,2,3,4) == Shape{});

Taking arbitrary slices of a Nested<T> object is significantly more complicated on account of the fact that slice requests for any of the inner layers will in general be slicing multiple tensors simultaneously. For example consider s2_2 from the previous code snippet. Slicing layer 0 is straightforward, asking for say {1,0}, {2,2} selects row 1 of the outer matrix. Generalizing, something like {1,0,5,5}, {2,2,10,10} would grab row 1 of layer 0, and rows 5 through 9 (inclusive) for each inner matrix. What if we wanted the first 5 rows of outer element {1,0} and the last 3 rows of outer element {1,1}? This request requires more than just a block range, it requires a JaggedShape. The above request can be requested by:

// The shape resulting from taking the first 5 rows of a 10 by 10 matrix
Shape e10({5,10}, {0,0});
// The shape resulting from taking the last 5 rows from a 10 by 10 matrix
Shape e11({3,10}, {7,0});
// A 1 row matrix with 2 columns whose elements are a 5 by 10 and a
// 3 by 10 matrix, the origin of the outer tensor is {1,0}
JaggedShape slice({{e10, e11}}, {1,0});

auto requested_slice = s2_2.slice(slice);

assert(requested_slice == slice);

As this also shows, requesting such slices also completely negates the point of the slice member because the input is the result. As a result, we have not designed such an API. Instead the slicing APIs for a Nested object are:

Nested<Shape> s2_2({2, 2}, Shape{2, 2, 10, 10});
Shape s01({1, 1, 10, 10}, {0, 1, 0, 0});

// Grabs the 0,1 element of the outer matrix preserving the rank
assert(s2_2.slice(0, 1) == Nested<Shape>({2, 2}, s01));

// Grabs the bottom row of the outer matrix, and the bottom 5 rows of
// the inner matrices
Nested<Shape> s1050({1, 2, 5, 5}, {1, 0, 5, 0});
s2_2.slice({1, 0, 5, 0}, {2, 2, 10, 10});

Ultimately, bear in mind, chipping and slicing are little more than convenience functions for working out the shapes resulting from slicing/chipping the tensor; for complicated selections it should always be possible to build the resulting shape manually.

Iterating

By default the origin of a freshly constructed shape is the zero vector. For slices and chips, the origin is the first element in the slice or chip (note that in the previous section we conveniently chose our slices/chips so the origin was the zero vector). By default, when iterating over a shape indices are returned as offsets from the origin, in lexicographical order. For example:

auto print_shape = [](auto&& s){
   for(const auto& index : s)
      std::cout << "{" << index[0] << "," << index[1] << "} ";
};

Shape s{2, 3};
print_shape(s);  // prints {0,0} {0,1} {0,2} {1,0} {1,1} {1,2}

auto s01_13 = s.slice({0, 1}, {1, 3});
print_shape(s01_13); // prints {0,1}, {0,2} NOT {0,0} {0,1}

// If we wanted {0,0} {0,1}
print_shape(s01_13.offsets());

// We can move the origin
s.set_origin({10, 10});
print_shape(s); // prints {10,10} {10,11} {10,12} {11,10} {11,11} {11,12}

For completeness we define overloads of Shape and JaggedShape which also take an origin. For JaggedShape the origin needs to be specified for the internal shapes and the explicitly unrolled ranks.

// Makes a shape for a 2 by 3 matrix whose first element is {10, 10}
Shape s({2, 3}, {10, 10});

// Outer vector starts at 10, element 11 of the outer vector starts at 5,
// element 12 of the outer vector starts at 6
JaggedShape js({{Shape({10}, {5}), Shape({20}, {6})}, {10});

// Outer vector starts at 10, inner vectors start at 10.
Nested<Shape> s1_1({1, 1}, s);

Summary

The design of the shape component satisfies the considerations raised above by:

Basic operations: The ShapeBase class will provide a common API for getting/setting basic information and performing common operations.
Nested: The Nested class tracks how the modes of a tensor are layered.
Jagged-ness: The JaggedShape class is used to represent jagged shapes.
Combining shapes: The IndexedShape class allows us to easily compose shapes.
Iterable: The various classes define iterators which allow users to iterate over the indices contained in the shape.

Additional Notes

Slicing and chipping assume contiguous sub-tensors. For grabbing noncontiguous sub-blocks and using them as if they were contiguous, one needs a mask.