Overview of TensorWrapper

This section provides a high-level overview of TensorWrapper’s architecture.

What is TensorWrapper?

There are a number of existing tensor libraries, with a variety of useful features; however, to our knowledge no existing tensor library has all the tensor features a high-performance physics or chemistry code may encounter. TensorWrapper is designed to provide a high-level, user-friendly, domain specific language (DSL) on top of existing tensor libraries, while abstracting away as much complexity as possible.

Why do we need TensorWrapper?

Tensors are the “DSL of physics” because nearly every law of physics is succinctly summarized by a tensor equation. That said, naively creating arrays of floating-point values and then subjecting them to the mathematical operations implied by the equations often leaves much performance on the table (especially when those operations are performed on heterogeneous high performance computers). Nonetheless we argue that having a tensor-based DSL is important for physics-based codes because it:

• Facilitates translating theory to code.

• Encapsulates mathematical optimizations.

• Code is easier to read/rationalize about.

Most existing tensor libraries are capable of achieving high-performance, but in many cases can only do so in certain cases or by “breaking API”. The need to break API complicates the use of those libraries and places much onus on the programmer. The goal of TensorWrapper is to provide a middle layer between existing tensor libraries and the user. By adding a middle layer we can better decouple the interface from the details.

Architecture Considerations

TensorWrapper’s overall architecture is motivated by the workflow we expect our users to adopt and the workflow we expect TensorWrapper to actually follow in order to performantly meet our user’s needs.

At the highest level, end users of TensorWrapper want to do four things. In order:

Set tensor properties

Before we even fill in a tensor we need to specify the properties of the tensor, i.e., its shape, permutational symmetries it may have, and its sparsity pattern.

• In this step we are really looking to specify “intrinsic” properties of the tensor. These properties define how the user is thinking of the tensor.

• Performance considerations will modify how the requested tensor is actually implemented and are discussed below (see Performance Considerations).

• Sparsity is also sometimes enforced after the fact by “knocking out zeros”. Such a process can be thought of starting the four steps over after we have created the tensor.

• For performance reasons, the tensor will need to know about the runtime it will live in.

• Much of this information is optional, but not supplying it will have performance implications.

Create a tensor

Once we have specified the properties of the tensor. We can allocate and fill in the elements of the tensor.

• Elements of a tensor usually result from an operation which takes the element’s indices as input.

• There are a number of notable “special” tensors like the zero and identity tensors which users will sometimes need to create too.

• Part of creating the tensor is selecting the backend. Ideally, TensorWrapper would be able to pick the backend most appropriate for the requested calculation; however, it is likely that for the forseeable future users will need to specify the backend, at least for the initial tensors (tensors computed from the initial tensors will use the same backend).

Compose with tensors

With a series of initialized tensors the user then expresses tensor operations.

• Standard mathematical operations: add, subtract, and contract

• Element-wise operations, e.g., square each element.

• Slicing

• Permuting

Compute results

After expressing the operations they want to do. The user expects to be able to have the operations evaluated - hopefully, in an efficient manner.

Performance Considerations

While the end-user considerations afford a nice user workflow, the reality is more needs to go into the tensor workflow to accomplish what the user wants in a performant manner. These “performance” steps should be interlaced between the “user” steps introduced in the previous section. Ideally, with automation, the “performance” steps can be merged into the “user” steps surrounding it. In the initial implementation of TensorWrapper, the intermediate steps must also be done by the user.

Runtime aware properties

The shape, symmetries, and sparsity of the tensor provided by the user will ultimately be “logical” and should reflect the problem being modeled. Under the hood, the actual properties of the tensor may vary widely depending on the runtime conditions.

• The actual properties depend on the runtime conditions, whereas the logical properties only depend on the problem.

• Actual shapes usually involve some sort of tiling for distribution across nodes and devices.

• How to distribute tiles (if they exist) for performance will need to be determined.

• Sparsity objects will need to be updated to account for the actual shape.

Runtime aware allocation

Where we put the tensor (e.g., CPU vs. GPU and RAM vs. disk vs. generated on-the-fly) can depend on the runtime status. Similarly the back end we choose (particular whether it is distributed or replicated) depends on the runtime as well as the extent of the tensor.

Runtime expression optimization

Certain optimizations of an equation (like collecting common terms) can in theory be done statically by analyzing the equations and trying to minimize the overall computational complexity. Other optimizations are tied to runtime conditions and thus can only be done in the context of the current runtime (or with a preconceived notion of what the runtime will look like).

• The order of contraction depends on the extent of each mode. Extents aren’t known until runtime.

• Factoring out on-the-fly tensors requires knowing they will actually be generated on-the-fly.

Out of Scope Considerations

Static expression optimization

Runtime expression optimization brought up the fact that some expression optimizations can happen simply given the equations. Such optimizations can be decoupled from TensorWrapper by using code generators to write expressions using TensorWrapper’s DSL.

Domain-specific optimization

In electronic structure theory (one of the motivators of TensorWrapper) it is possible to simplify equations based on the electron’s spin or the spatial symmetry of the molecular system. Historically, it has been common to build these optimizations into the math layer, but this in turn makes the math layer less reusable. Furthermore, things like spin symmetry and spatial symmetry often simply result in tensor sparsity. Point being, many of these optimizations can be mapped to more general tensor considerations.

• To be clear, designing interfaces explicitly for domain-specific optimizations is out of scope. The underlying optimizations (usually sparsity and symmetry) are in scope.

Architecture Design

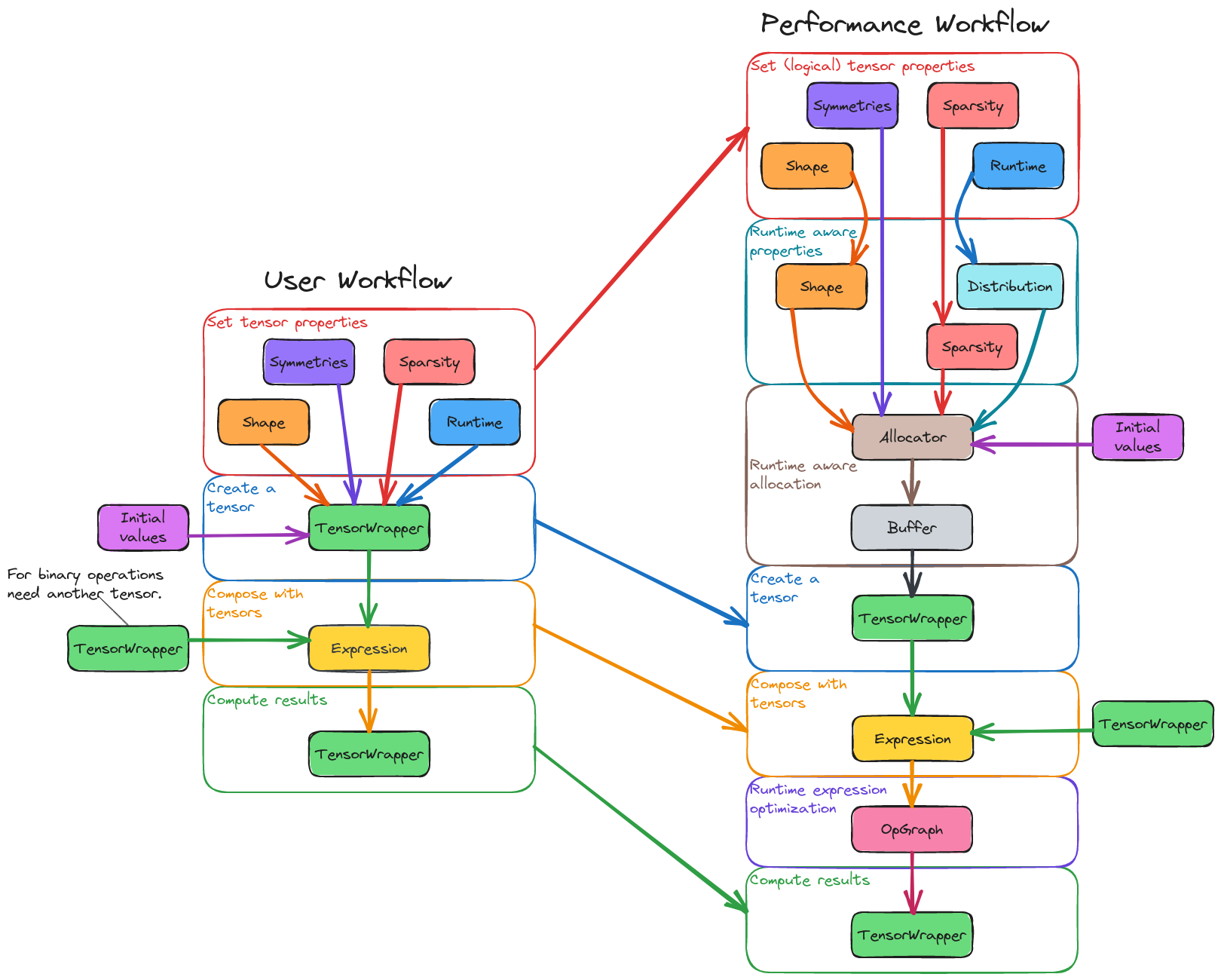
Fig. 4 Left. The ideal user-based workflow for using TensorWrapper. Right. The user-based workflow with performance-inspired steps interjected.

Section Architecture Considerations presented two workflows: a user-based and a performance-based workflow. Fig. 4 illustrates these workflows using the major pieces of TensorWrapper. As mentioned in the previous section, the end goal is to have the performance-focused workflow be an implementation detail. For example, the Runtime aware properties and Runtime aware allocation steps could occur within the constructor of the TensorWrapper class. Similarly, the Runtime expression optimization step could be triggered when a TensorWrapper object is initialized by an Expression object.

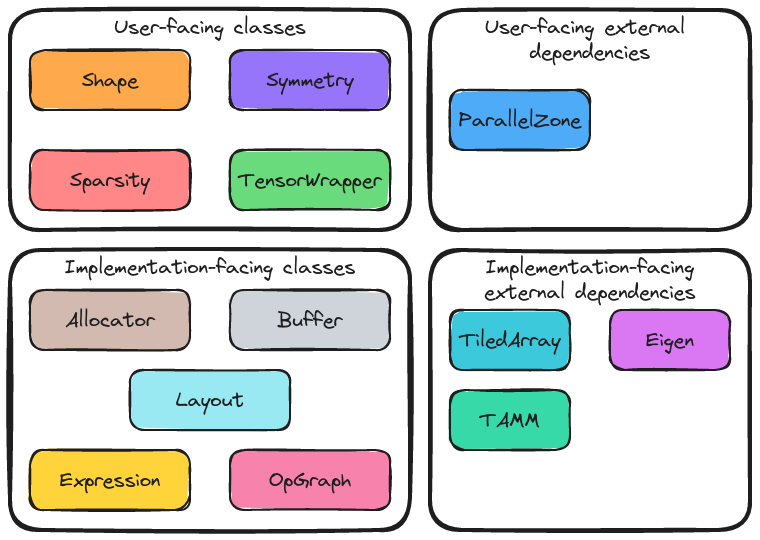
Fig. 5 The architecture of TensorWrapper.

Fig. 5 shows the major components of TensorWrapper. The components are organized into four categories, based on whether they are part of TensorWrapper or a dependency and whether they are user-facing or implementation-facing.

User-Facing Classes

As motivated by Fig. 4, users of TensorWrapper primarily interact with four components:

Shape

Main discussion: Tensor Shape Design.

Tensors are thought of as hyper-rectangular arrays of elements. The Shape component is responsible for describing this array of values. In particular the Shape component is responsible for representing:

• rank of the tensor

• extent of the tensor

• nesting structure of the hyper-rectangular arrays

• converting indices from one shape to indices in another shape

Symmetry

Main discussion: Designing the Symmetry Component.

In practice many of the tensors commonly encountered have some sort of permutational symmetry. While such symmetry could be discovered by inspecting the tensor, it is more common to have the user specify it. The Symmetry component is charged with storing the symmetry relationships and providing helpful tools for exploiting it. In particular the Symmetry component is responsible for:

• Symmetry and antisymmetry (real elements)

• Hermitian and anti-Hermitian (complex elements)

• Other symmetry mappings

Sparsity

Main discussion: Tensor Sparsity Design.

While symmetry deals with telling us which elements must be the same (up to a sign), sparsity deals with telling us which elements are zero. The Sparsity component is responsible for dealing with:

• tracking element-wise sparsity (N.B. tile sparsity is element-sparsity in a nested tensor)

• switching among sparsity representations

• Nesting of sparsity

As a note, in TensorWrapper tiling implies a nested tensor. Therefore tile- sparsity is actually element-sparsity, just for non-scalar elements. The point is, even though we anticipate tile-sparsity to be the most important sparsity we think that TensorWrapper needs to be designed with element-sparsity in mind from the get go.

TensorWrapper

Main discussion: Designing TensorWrapper Class.

The TensorWrapper class is the tensor-like object that users interact with. The DSL uses TensorWrapper objects as the leaf nodes of an abstract syntax tree (AST). To users, the main responsibilities of the TensorWrapper component are:

• storing the data

• providing an entry point into the DSL.

User-Facing External Dependencies

TensorWrapper additionally needs a description of the runtime. For this purpose we have elected to build upon ParallelZone.

Implementation-Facing Classes

As shown in Fig. 4 and Fig. 5, the Performance Considerations lead TensorWrapper to have several additional components. These components are required to convey additional state necessary for performance.

Allocator

Main discussion: Designing the Allocator.

The Allocator component wraps the process of going from the actual Shape, Sparsity, and Symmetry for the tensor to an object of the backend library. Appropriate selection of the allocator determines things such as:

• Fundamental type of the values (e.g., float, double, etc.)

• Vectorization strategy (row-major vs. column-major)

• Value location: distribution, RAM, disk, on-the-fly, GPU

Buffer

Main discussion: Designing the Buffer.

To the extent possible TensorWrapper strives to avoid needing to reimplement tensor math routines. Key to these efforts are the already existing tensor libraries. The Buffer component is responsible for providing a unified interface into which the various backends can be attached. The main goals of the buffer are:

• Type-erase the backend.

• Record data runtime location

• Opaquely move data

Layout

Main discussion: Designing the Layout Component.

The Shape provided by the user is the shape of the tensor’s values based on the problem. The Symmetry object tells us which of those values are independent. And the Sparsity object tells us which values are zero. For performance reasons TensorWrapper may opt to actually allocate the tensor with different properties. The Layout component is responsible for describing the runtime properties of the tensor:

• Actual shape of the tensor (including tiling)

• Actual symmetry (accounting for actual shape)

• Actual sparsity of the tensor (accounting for symmetry)

• Distribution for distributed tensors

Expression

Main discussion: Designing the Expression Component.

Like most tensor libraries, TensorWrapper will rely on an expression layer for composing tensor expressions. Strictly, speaking this layer is entered into in a user-facing manner; however, the expression layer is specifically designed to appear to the user like they are working with only TensorWrapper objects, which is why we consider it an implementation detail. Responsibilities include:

• Assembling the concrete syntax tree (CST) from the domain specific language (DSL).

• Express transformations of a single tensor

• Express binary operations

• Represent branching nodes of the abstract syntax tree (AST)

OpGraph

Main discussion: Designing the OpGraph.

The Expression component contains a user-friendly mechanism for composing tensors using TensorWrapper’s DSL. The result is a concrete syntax tree (CST). In practice, CSTs contain extraneous information (and in C++ are typically represented by heavily nested template instantiations which are not fun to look at). The OpGraph component is designed to be an easier-to-manipulate, more-programmer-friendly representation of the tensor algebra the user requested than the Expression component. It is the OpGraph which is used to drive executing the backends. Responsibilities include:

• Converting the concrete syntax tree (CST) to an abstract syntax tree (AST)

• Runtime optimizations of the abstract syntax tree (AST)

Implementation-Facing External Dependencies

TensorWrapper is designed to wrap existing high-performance tensor libraries into a common domain specific language (DSL) and to exploit the advantages of each of these libraries in an interoperable manner. The interfaces to these various backends live in this component.