Designing the Symmetry Component
The point of this page is to capture the considerations which went into designing the symmetry component of TensorWrapper.
What is (tensor) symmetry?
Consider a matrix \(\mathbf{T}\), we say \(\mathbf{T}\) has symmetry if given element \(t_{ij}\) we know the value of a different element of \(\mathbf{T}\), say \(t_{ab}\). One of the more common types of symmetry is when \(\mathbf{T}\) is a symmetric matrix, in which case \(t_{ij} = t_{ji}\).
For our purposes, given a tensor \(\mathbf{T}\), a symmetry \(S\) is a mapping of the elements comprising a slice of \(\mathbf{T}\), \(\mathbf{t}\), to those same elements (up to a sign) in another slice \(\mathbf{t'}\). We are specifically interested in non-trivial mappings where \(\mathbf{t}\) and \(\mathbf{t'}\) are not given by the same offsets. In the common scenario of permutational symmetry, \(\mathbf{t}\) and \(\mathbf{t'}\) will be slices containing a single element, but for other symmetries \(\mathbf{t}\) may contain more than one element. Strictly speaking \(\mathbf{t}=\mathbf{0}\) satisfies our definition of a symmetry; however, such symmetries are usually treated differently on account of the special properties of zero (namely its trivial multiplication and addition). The case when \(\mathbf{t}=\mathbf{0}\) is usually referred to as “sparsity” and is considered in Tensor Sparsity Design.
Why do we need to consider symmetry?
Performance. While we can always fill the tensor with the symmetrically equivalent elements and then subject the tensor to standard tensor operations without symmetry, doing so leads to a lot of wasted memory and also leads to a large amount of redundant work. By understanding the symmetry of the tensor we can avoid this additional work.
Symmetry Considerations
- Symmetric and antisymmetric
As far as we know, permutational symmetry is the most common type of tensor symmetry. Permutational symmetry occurs when the symmetry operation maps the input slice to an output slice with the same indices just permuted. A common example is a symmetric matrix where an element \(t_{ij}\) is equal to \(t_{ji}\).
In tensors with rank greater than 2, symmetric/antisymmetric modes are sorted into sets. The full set of symmetry equivalent elements is generated by considering all possible permutations of the set.
Sets of symmetric/antisymmetric modes are not necessarily disjoint; however, no pair of modes can appear in more than one set.
Generalizes to Hermitian/anti-Hermitian if elements are complex.
The same tensor can have both symmetric and antisymmetric modes.
Pairwise mode permutations are most common, but it is also possible that permutations must be ternary (e.g., cyclic permutations of three- dimensional space) or higher.
- Translational symmetry
As a disclaimer, we could not find a name for this sort of tensor symmetry and thus coined our own. Thinking of a tensor as a series of tiles, symmetries occur when any of those tiles are the same. If we only stored one copy of each symmetry unique tile, we could then form the entire tensor by translating the symmetry unique tiles to each of the symmetry redundant positions. For permutational symmetry, the indices of the symmetry redundant tiles must be the same as the the indices of the symmetry unique tile, up to a permutation. However, our translation algorithm suggests that in general other translations will be needed, specifically translations where the input and output indices are not related by permutations. We term such symmetries as translational.
Can arise when basis vectors are products and the value of the tensor’s elements only depend on part of the basis vector.
In general are specified by providing the input slice and the output slice.
- Basic properties
Users interacting with classes in the symmetry component will want access to:
Which elements are symmetry unique/redundant.
Whether an element is symmetry unique/redundant.
For a given shape, how many elements are symmetry unique/redundant.
The sign of the resulting element.
- Composition
When combining two tensors \(\mathbf{A}\) and \(\mathbf{B}\) to form \(\mathbf{C}\), the symmetry of \(\mathbf{C}\) is determined from the symmetry of \(\mathbf{A}\) and \(\mathbf{B}\). The symmetry component should be able to compose symmetries using Einstein notation, just like the tensors the symmetries describe.
Out of Scope Considerations
- Sparsity
Based on our definition of symmetry, sparsity is a symmetry; however, users typically think of it differently, plus it internally is used differently. For these reasons we consider sparsity separately from symmetry. For full design details of the sparsity component see Tensor Sparsity Design.
- Exploiting symmetry
The point of the symmetry component is to provide the user a mechanism for expressing the symmetry of the tensor. Choosing what elements to store is part of the physical layout (see Designing the Layout Component) and actually exploiting the symmetry of the tensor is left to the backend.
Symmetry Design
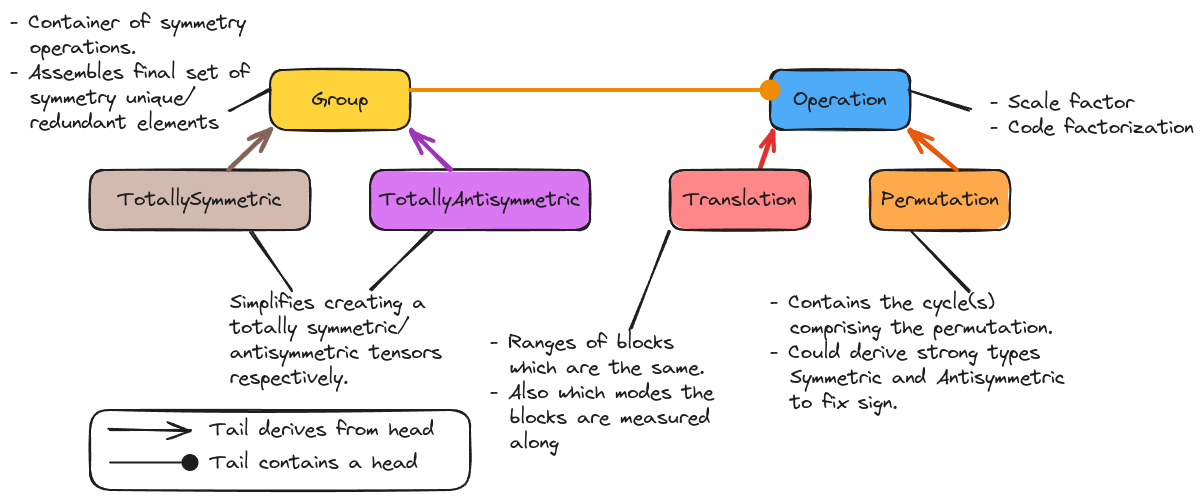
Fig. 7 The major classes involved in the symmetry component.
Fig. 7 shows the classes primarily responsible for defining
the symmetry component. Ultimately the user assembles a Group object,
which describes all of the tensor’s overall symmetries. It is the Group
object which is used by the rest of TensorWrapper. The remaining classes of
the Group class hierarchy exist primarily to help the user create the
Group object in a straightforward manner.
TotallySymmetricallows a user to declare a tensor as totally symmetric simply by providing the rank of the tensor.TotallyAntiSymmetricallows a user to declare a tensor as totally antisymmetric simply by providing the rank of the tensor.
Ultimately the symmetry of a tensor is mathematically treated using group
theory. The symmetry operations on the tensor being the members of the group.
Group is thus a container filled with Operation objects (symmetry
namespace distinguishes between other Operation classes; in practice users
interact with derived classes which have more descriptive names). All symmetry
operations derive from Operation, which serves primarily to
provided a consistent API among the various operations and to provide some
code factorization.
Permutation is used to model both symmetry and antisymmetric permutations
of modes (the difference being described by a scale factor). Internally
Permutation stores the cycle(s) comprising the permutation.
The final symmetry operation is Translation. The inputs to a Translation
object are two or more Shape objects (JaggedShape and Nested work
too). The input objects are treated as ranges, and indicate which slices or
chips of the tensor which must have the same values. Conceptually it is
possible to specify any symmetry in this manner, but it is very tedious (e.g.,
specifying that an \(n\) by \(n\) matrix is symmetric using
Translation objects requires creating \(n\choose 2\) Translation
objects, one for every pair of symmetry related elements).
Proposed APIs
Constructing Permutational Symmetry Objects
Non-trivial permutational symmetry requires minimally a rank 2 tensor. The
Permutation object can still be constructed for ranks less than 2. The
relevant Permutation ctors:
// Permutation of 0 modes
Permutation p0;
// Permutation of the 0-th mode with itself (i.e., a fixed-point). p1 is the
// same as p0 an identity permutation
Permutation p1(0);
Declaring non-trivial permutations:
// Permutes modes 0 and 1
Permutation p01{0, 1};
// Cyclic permutation of modes 0, 1, and 2
Permutation p012{0, 1, 2};
// Permutations can be made up of multiple disjoint cycles, e.g., this
// permutation sends mode 0 to mode 2 and mode 1 to mode 3
Permutation p02_13{{0, 2}, {1,3}};
Group objects are simply containers of Operation objects. So
construction looks like:
// Symmetry group of the empty set, i.e., the basis set of a scalar
Group g0;
// Symmetry group of a vector (will be the same as g0 because Groups store
// identity operations implicitly)
Group g1(Permutation{0});
// Symmetry group of a matrix with no permutational symmetry (same as g0 and
// g1 because identity is not stored)
Group g2(Permutation{0}, Permutation{1});
// Symmetry group of a symmetric matrix
Group g2_symmetric(Permutation{0, 1});
// Symmetry group of a tensor where modes 1 and 2 are symmetric (specifying
// Permutation{0} is NOT required)
Group g3(Permutation{0}, Permutation{1, 2});
Note
Design from this point forward is speculative and not yet implemented.
Other possible rank 3 constructions are:
// Modes 0 and 1 are symmetric, modes 0 and 2 are antisymmetric
Group s01_a02(Symmetric{0, 1}, Antisymmetric{0, 2});
// Modes 0 and 1 are symmetric, modes 1 and 2 are antisymmetric
Group s01_a12(Symmetric{0, 1}, Antisymmetric{1, 2});
// Modes 0 and 2 are symmetric, modes 0 and 1 are antisymmetric
Group s02_a01(Symmetric{0, 2}, Antisymmetric{0, 1});
// Modes 0 and 2 are symmetric, modes 1 and 2 are antisymmetric
Group s02_a12(Symmetric{0, 2}, Antisymmetric{1, 2});
// Modes 1 and 2 are symmetric, modes 0 and 1 are antisymmetric
Group s12_a01(Symmetric{1, 2}, Antisymmetric{0, 1});
// Modes 1 and 2 are symmetric, modes 0 and 2 are antisymmetric
Group s12_a02(Symmetric{1, 2}, Antisymmetric{0, 2});
// N.B. order of symmetric and antisymmetric in constructor does not matter
// so the other 6 mixed symmetric/antisymmetric possibilities are the same
// just with Antisymmetric being the first argument and Symmetric the
// second.
// Totally antisymmetric rank 3
Group a012(Antisymmetric{0, 1, 2});
For the special cases of totally symmetric and totally antisymmetric additional classes exist which facilitate construction:
TotallySymmetric s; // Null totally symmetric object
TotallySymmetric s0(0); // Totally symmetric scalar
TotallySymmetric s1(1); // Totally symmetric vector
TotallySymmetric s2(2); // Totally symmetric matrix
TotallySymmetric s3(3); // Totally symmetric rank 3 tensor
TotallyAntisymmetric a; // Null totally symmetric object
TotallyAntisymmetric a0(0); // Totally antisymmetric scalar
TotallyAntisymmetric a1(1); // Totally antisymmetric vector
TotallyAntisymmetric a2(2); // Totally antisymmetric matrix
TotallyAntisymmetric a3(3); // Totally antisymmetric rank 3 tensor
Once we consider rank 4 and higher we can also have multiple symmetric (or antisymmetric) categories, for example:
Group s01_s23(Symmetric{0, 1}, Symmetric{2, 3});
A Symmetric, Antisymmetric, or Asymmetric object given n modes,
stands for all n choose 2 possible mode pairs that can be formed from the
n modes in it, i.e., s01_s23 is NOT the same as:
Group s0123(Symmetric{0, 1, 2, 3});
because s0123 additionally has symmetries among 0 and 2, 0 and 3,
1 and 2, and 1 and 3, which are not present in s01_s23.
Constructing Group Objects with Translational Symmetry
For specifying permutational symmetry we needed to state the modes to permute. For translational symmetry we need to specify which blocks are equivalent:
// Block 0 starts at {0,0} and ends at {10,10}
// Block 1 starts at {10,10} and ends at {20,20}
// Block 2 starts at {20,20} and ends at {30,30}
Shape block0{10, 10}, block1({10, 10}, {10, 10}), block2({10, 10}, {20, 20});
// matrix where block0 is the same as block1
Group b0b1(Translation{block0, block1});
// matrix where block0 is the same as block1 and block2
Group b0b1b2(Translation{block0, block1, block2});
// Just like permutational symmetry where only some of the modes need to
// be involved, we can have translational symmetry which only involves a
// subset of the modes. In this case we need to specify which modes the
// indices are associated with. The following declares a Group object
// for a rank 3 tensor where modes 0 and 1 have translational symmetry such
// that the block0 slice is the same as the block1 slice
Group b0b1(3, Translation({block0, block1}, {0, 1}));
Translational symmetry can also be declared for more exotic ranges, such as those involving jagged and/or nested:
// Block of a jagged matrix where row 0 is 10 elements long and row 1 is 20
JaggedShape jblock0{Shape{10}, Shape{20}};
// Block of a jagged matrix where row 2 is 10 elements long and row 3 is 20
JaggedShape jblock1({Shape{10}, Shape{20}}, {2});
// Symmetry for a jagged matrix where block0 and block1 must be the same
Group b0b1(Translation{jblock0, jblock1});
// Outer vector 10 elements long, inner are 20
Nested<Shape> nblock0({1,1}, Shape{10, 20});
// Same shape, but the first index of the first inner vector is 20 not 0
Nested<Shape> nblock1({1, 1}, Shape({10, 20}, {0, 20}));
// Symmetry for a rank 4 tensor where modes 0 and 1 are nested
Group nb0nb1(4, Translation{nblock0, nblock1}, {0, 1});
Note that the fact that Translation describes a symmetry operation means
that the shapes in the symmetry operations must be the same up to a translation
of the origin. The shapes will also need to be consistent with the shapes of
the respective modes of the tensor. Finally, we note that it’s possible to
combine all of these mechanisms:
// two 1 by 1 shapes, one with origin (0, 0) the other with origin (1,1)
Shape e00{1, 1}, e11({1, 1}, {1, 1});
// Rank 4 tensor, slice is the same as the (1,1) slice and modes 2 and
// 3 are symmetric
Group sym(Translational({e00, e11}, {0, 1}), Symmetric{2, 3});
Basic Properties
While I have some idea of what properties will be needed, how to best expose them is punted until I have a better idea of how they would be used under the hood.
Summary
- Symmetric and antisymmetric
The
Permutationclass has been introduced to facilitate expressing permutations.- Translational symmetry
The
Translationclass describes slices of the tensor which are the same.- Basic properties
This is one of the primary responsibilities of the
Groupclass.
Additional Notes
Can we use jagged tensors here? In particular I’m thinking an upper-triangular matrix without the lower triangle is a jagged matrix.
I believe that symmetry can be completely implemented without needing to store the tensor’s overall shape (
Translationalwill need the shapes of the blocks, but shouldn’t need the overall shape).