Tensor Sparsity Design

This page documents the process of designing the sparsity component of TensorWrapper.

What is tensor sparsity?

In the context of tensors, sparsity refers to tensors possessing elements which are effectively zero. Exactly what defines the effective zero is situational and problem-specific. The sparsity component is responsible for indicating which elements are zero or non-zero, not only in a single tensor, but also in tensor expressions.

Why do we need tensor sparsity?

If a tensor exhibits a substantial amount of sparsity, then implicitly storing the zero values leads to a significant space savings. Furthermore, because of the special properties of zero, e.g., \(\mathbf{T}+\mathbf{0}=\mathbf{T}\) and \(\mathbf{T}\mathbf{0}=\mathbf{0}\), many tensor operations involving sparse tensors can be done implicitly.

Sparsity considerations

Element Sparsity

Element sparsity is concerned with specifying whether each individual element of a tensor is zero/non-zero. An element sparse tensor has isolated non-zero elements, each surrounded by a “sea” of zero elements.

• Effectively exploiting element sparsity requires custom linear algebra routines designed to act element-wise, rather than on contiguous blocks.

• In theory, TensorWrapper could look at a provided element sparsity, back out a block-sparsity (vide infra), and use whichever sparsity leads to better performance, but for now TensorWrapper assumes the user has already done such an analysis.

Block Sparsity

Block sparsity is concerned with specifying whether multi-element slice and chip of a tensor are all zero of if they contain non-zero elements. It should be noted that a slice/chip is zero only if every element in the chip is zero too. Since slices/chips can contain a single element the distinction between element and block sparsity is not always clear. Simply put, element vs block sparsity comes down to whether the user provided the sparsity component with single elements or chips/slices.

• Exploiting block-wise sparsity can only be done with block-wise operations (either involving chips or slices).

• Block-wise operations are either done manually by interacting with slices/chips of a tensor, or automatically when an operation involves a nested tensor.

• As a result of the previous point, tensors declared with either a JaggedShape or a Nested shape benefit most from block sparsity. Here it should be noted that the former has an implicit nesting resulting from the boundary between the jagged and smooth ranks, whereas the latter has explicit nestings.

Effective Sparsity

In practice we are not only concerned with hard zeros (elements, slices, or chips which are identically zero), but also values which are so small that for all intents and purposes they are zero. The sparsity component needs to exploit this effective sparsity as well.

Operational Sparsity

Given an operation combining two tensors, \(\mathbf{A}\) and \(\mathbf{B}\), to form \(\mathbf{C}\) we need to be able to work out the sparsity of \(\mathbf{C}\) from the sparsity of \(\mathbf{A}\) and \(\mathbf{B}\).

• To work out the sparsity of \(\mathbf{C}\) we need the shapes of \(\mathbf{A}\) and \(\mathbf{B}\). Having the symmetry makes it potentially more efficient.

Effective Operational Sparsity

Given two tensors, \(\mathbf{A}\) and \(\mathbf{B}\), which are not sparse, it is possible to combine \(\mathbf{A}\) and \(\mathbf{B}\) to form \(\mathbf{C}\), and have \(\mathbf{C}\) be sparse. Of particular note, is when \(\mathbf{A}\) and \(\mathbf{B}\) contain values with magnitudes between 0 and 1, in which case the elements of \(\mathbf{C}\) will have even smaller magnitudes than those in either \(\mathbf{A}\) or \(\mathbf{B}\).

• Another important case is subtraction; if \(\mathbf{A}\) and \(\mathbf{B}\) are approximately equal then their difference will be approximately zero. This is particularly important for iterative methods where converged elements do not change among iterations.

• Sparsity may arise through addition, if \(\mathbf{A}\) and \(\mathbf{B}\) have opposite signs. In this case the resulting sparsity is similar to that which results from subtraction.

• Exploiting effective operational sparsity requires use of inequalities such as Cacuchy-Schwarz. For elemental sparsity these inequalities must be considered element by element and offer no cost savings over simply carrying out the operation and inspecting the result (n.b., that inspecting the result, \(\mathbf{C}\), for additional sparsity can be useful if \(\mathbf{C}\) is used later). For block sparsity, inequalities can be checked by using block norms. If the norms fail the inequality then it is possible to avoid forming the full sparse block.

Dual problem

Since a sparse tensor has a lot of zeros, sparsity specification is usually thought of in terms of specifying the non-zero elements. Since a given tensor element is either zero or non-zero, we can just as easily think of sparsity specification via the dual problem, i.e., specifying the zero elements of a tensor. Users will in general prefer to to specify the sparsity which ever way is quicker.

• Even if a tensor is predominantly dense, exploiting sparsity, particularly block sparsity, can still lead to major performance improvements.

• In order to be able to switch between representations we need to know the overall shape of the tensor.

Symmetry

Knowing the symmetry of the tensor allows us to know where zero/non-zero elements are with less information.

Basic Operations

In addition to constructing a representation of a tensor’s sparsity we also need to know:

• Whether an element/range of elements is zero or not.

• The fraction of zero elements (i.e., the sparsity).

• Unions of sparsity objects (for algorithm purposes and useful for building up the final sparsity).

Not in Scope

Storage format

A number of schemes exist for storing sparse tensors, e.g., compressed sparse row and compressed sparse column. While the sparsity component will need to adopt one (or possibly multiple) formats, doing so is an implementation detail and not explicitly considered in the user-facing design.

Sparse Map

For a matrix, compressed sparse row format is a map from non-zero row indices to non-zero column indices. For example, if for a 3 by 3 matrix, row 0 has two non-zero elements, in columns 1 and 2, row 1 is only non-zero at column 0, and row 2 is zero. We can express this with the map {0 : {1, 2}, 1 : {0}}. For higher rank tensors, it is possible to compose these maps. For example, say that we want to map the rows in our original matrix to products of the columns, we then know that we only need to consider the components {0 : {{1, 1}, {1, 2}, {2, 1}, {2,2}}, 1 : {0.0}}.

• The real power of sparse maps comes in when you compose them over a series of expressions. In particular, given an expression and a series of sparse map objects, sparse maps can be used to create the element/block sparsity of the expression.

• As such, sparse maps are a mechanism for creating objects which live in the sparsity component and are not considered further here. Sparse maps are punted to Designing the Expression Component.

Sparsity Design

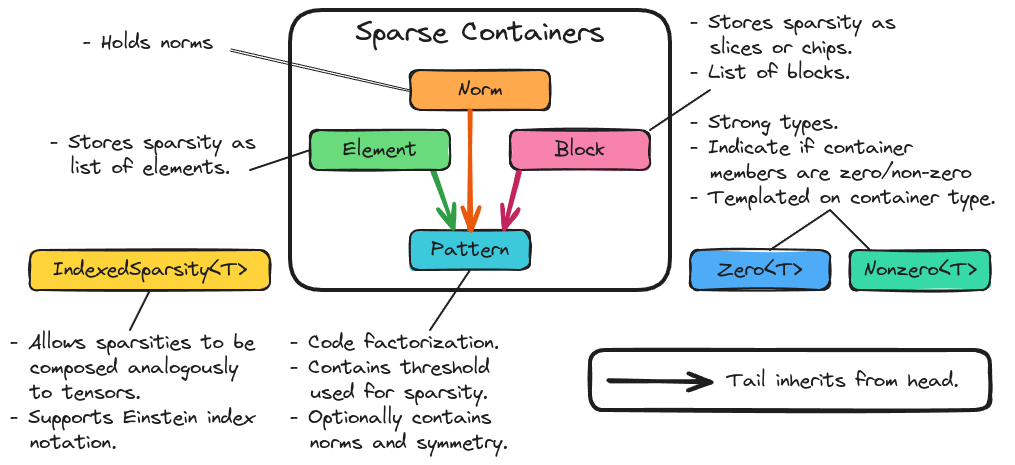
Fig. 8 The major classes underlying the sparsity component of TensorWrapper.

Fig. 8 shows the main components of TensorWrapper’s sparsity component. From considerations Element Sparsity and Block Sparsity we know that we expect users to specify sparsity in one of two ways. TensorWrapper represents each of these ways with its own container (respectively Element and Block). Ultimately these descriptions all contain the same information (whether pieces of a tensor are zero or not), just with different representations optimized for the various limits. In an attempt to treat these representations consistently, and to introduce code factorization, we have introduced a common base class Sparsity.

From the Dual problem consideration we know that the user may wish to fill these containers either with the zero elements of the tensor or with the non-zero elements of the tensor. We thus introduce two strong types Zero and Nonzero which are templated on the container type.

For determining the sparsity of an operation we introduce the IndexedSparsity class. Like the other indexed quantities, IndexedSparsity allows sparsity objects to be combined using Einstein notation.

Proposed APIs

Declaring an Element Object

Conceptually the simplest sparsity is elemental, which is represented by the Element class. Declaring a tensor has elemental symmetry requires the shape of the tensor and the zero/non-zero elements. By default Element assumes that the provided indices are for non-zero elements, you need to create Nonzero<Element> objects to denote that the indices are actually for the non-zero elements:

// A null sparsity object (no shape, no elements, no sparsity)
Element enull;

// Sparsity for a scalar which is zero
Element e0(Shape{}, {});

// Sparsity for a scalar which is non-zero
Element zero0(Shape{}, {{}});

// Sparsity for 10 element vector with all zero elements
Element zero1(Shape{10}, {});

// Sparsity for a 10 element vector with non-zero elements 3,5,7
Element e1(Shape{10}, {3, 5, 7});

// Sparsity for a 10 by 20 matrix with non-zero elements: (1,2), (2,3), and
// (3,4)
Element e2(Shape{10, 20}, {{1,2}, {2,3}, {3,4}});

// Sparsity for a 10 by 20 by 30 rank 3 tensor with non-zero elements:
// (1,2,3) and (2,3,4)
Element e3(Shape{10, 20, 30}, {{1,2,3}, {2,3,4}});

// Sparsity for a rank 4 tensor totally symmetric tensor with non-zero
// elements (1,2,3,4), (2,3,4,5), and (3,4,5,6)
Element e4(
   Shape{10, 20, 30, 40},
   {{1,2,3,4}, {2,3,4,5}, {3,4,5,6}},
   TotallySymmetric(4)
);

// To instead specify where the zeros are we use the Zero class template.
// This makes a 10 element vector where elements 3, 5, and 7 are zero:
Zero<Element> e1_0(Shape{10}, {3, 5, 7});

// N.B. Declarations of Nonzero<Element> objects are also allowed and are
// equivalent to just declaring Element objects, e.g. an equivalent way of
// specifying e2 is by:
Nonzero<Element> e2_2(Shape{10, 20}, {{1,2}, {2,3}, {3,4}});

// Shapes can be JaggedShape. This is the sparsity for a 3 row jagged matrix
// with columns of length 10, 20, and 30, where elements (0,3), (1,2), and
// (2,4) are non-zero.
Element je2(
   JaggedShape{Shape{10}, Shape{20}, Shape{30}},
   {{0,3}, {1,2}, {2,4}}
);

// Shapes can also be nested, element indices are flattened (if you don't
// want to flatten them use a sparse map). This is the same sparsity as je2
// except the corresponding tensor is now being thought of as a vector of
// vectors instead of a jagged matrix
Element je1_1(
   Nested<JaggedShape>({1,1}, JaggedShape{Shape{10}, Shape{20}, Shape{30}}),
   {{0,3}, {1,2}, {2,4}}
);

Initializer lists are nice for tutorials, but we expect most users will actually initialize sparsity objects from containers filled at runtime. For example:

/// Type Element uses
using size_type = Element::size_type;

// For a rank r tensor each index has r components. We will pass each index
// as a std::vector<size_type>, thus to provide a list of indices we need
// a vector of vectors.
std::vector<std::vector<size_type>> non_zeros = get_non_zeros();

// Sparsity for a 10 by 20 by 30 by 40 by 50 rank 5 tensor with non-zero
// elements specified by "non_zeros" instance.
Element e5(Shape{10, 20, 30, 40, 50}, non_zeros);

Declaring a Block Object

After element sparsity, block sparsity is the next simplest. Block sparsity is represented by the Block class. Block objects are created similar to Element objects except that instead of providing indices we provide the sub-shapes which are non-zero:

// Null block object (no shape, no blocks, no sparsity)
Block bnull;

// Sparsity for a zero scalar
Block b0(Shape{}, {})

// Sparsity for a non-zero scalar
Block zero0(Shape{}, {Shape{}});

// Sparsity for 10 element vector with non-zero elements: 1, 3, 4, 5, and 6.
Shape s1{10};
Block b1(s1, {s1.slice({1}, {2}), s1.slice({3}, {7})});

// Sparsity for a 10 by 20 matrix where the diagonal 5 by 10 blocks are
// non-zero
Shape s2{10, 20};
Block b2(s2, {s2.slice({0, 0}, {5,10}), s2.slice({5,10}, {10,20}));

// Sparsity for a 10 by 20 by 30 rank 3 tensor with two non-zero blocks:
Shape s3{10, 20, 30};
Block b3(
   s3, {s3.slice({0,0,0}, {10, 5, 8}), s3.slice({4, 7, 3}, {8, 9, 10})
);

// Shapes can be JaggedShape
JaggedShape js2{Shape{10}, Shape{20}};
Block jb2(js2, {js2.slice({0, 2}, {1, 8}), js2.slice({1, 4}, {2, 9})});

// or Nested<T>
Nested<Shape> s11({1,1}, Shape{10, 20});
Block b11(s11, {s11.slice({0, 3}, {1, 4}), s11.slice({1,4}, {6,5})});

Analogous to Element, one can specify the zero blocks by using Zero<Block> and the constructors also accept iterators over lists of shapes.

Declaring a Sparsity Object with Norms

Effective sparsity is conceptually a variation on block sparsity where instead of specifying whether each block is/isn’t zero, we instead specify “how zero” a block actually is. Put another way, Block objects are Norm objects where zero blocks have a norm of zero and and non-zero blocks have norms of infinity. Declaring a Norm object requires: the shape of the tensor, the norms of the blocks, and the effective zero threshold:

// Null Norm object (no shape, no sparsity)
Norm nnull;

// Norm object for a scalar
Norm n0(Shape{}, Tensor{norm});

// Norm object for a 10 element vector
Norm n1(Shape{10}, Tensor{norm}));

// Norm object for a 5 by 20 Matrix viewed as a vector of vectors
Nested<Shape> s1_1({1, 1}, Shape{5, 20});;
Norm n2(s1_1, Tensor{norm0, norm1, norm2, norm3, norm4}, 10E-10);

// Vector of matrices example
Nested<Shape> s1_2({1, 2}, Shape{5, 20, 30});
Norm n1_2(s1_2, Tensor{norm0, norm1, norm2, norm3, norm4});

// Matrix of vectors example
Nested<Shape> s2_1({2, 1}, Shape{3, 3, 10});
Tensor t{{norm00, norm01, norm02},
         {norm10, norm11, norm12},
         {norm20, norm21, norm22}};
Norm n2_1(s2_1, t);

// Jagged matrix with three rows
JaggedShape js2{Shape{10}, Shape{20}, Shape{30}};
Norm jn2(js2, Tensor{norm0, norm1, norm2});

As shown for n0, Norm works with Shape objects, but only supports a single norm (that of the entire tensor) in such cases. Generally speaking, Norm is much more useful for tensors declared with JaggedShape, Nested<Shape>, or Nested<JaggedShape> shapes. As also shown, the norms are provided as Tensor objects. The rank of the provided tensor is always zero if the Norm object is based off of a Shape object and it is the rank of the outer layer for JaggedShape and Nested objects. Finally, as shown in constructing n2 the user may provide a custom zero (default is machine precision).

Composing Sparsity Objects

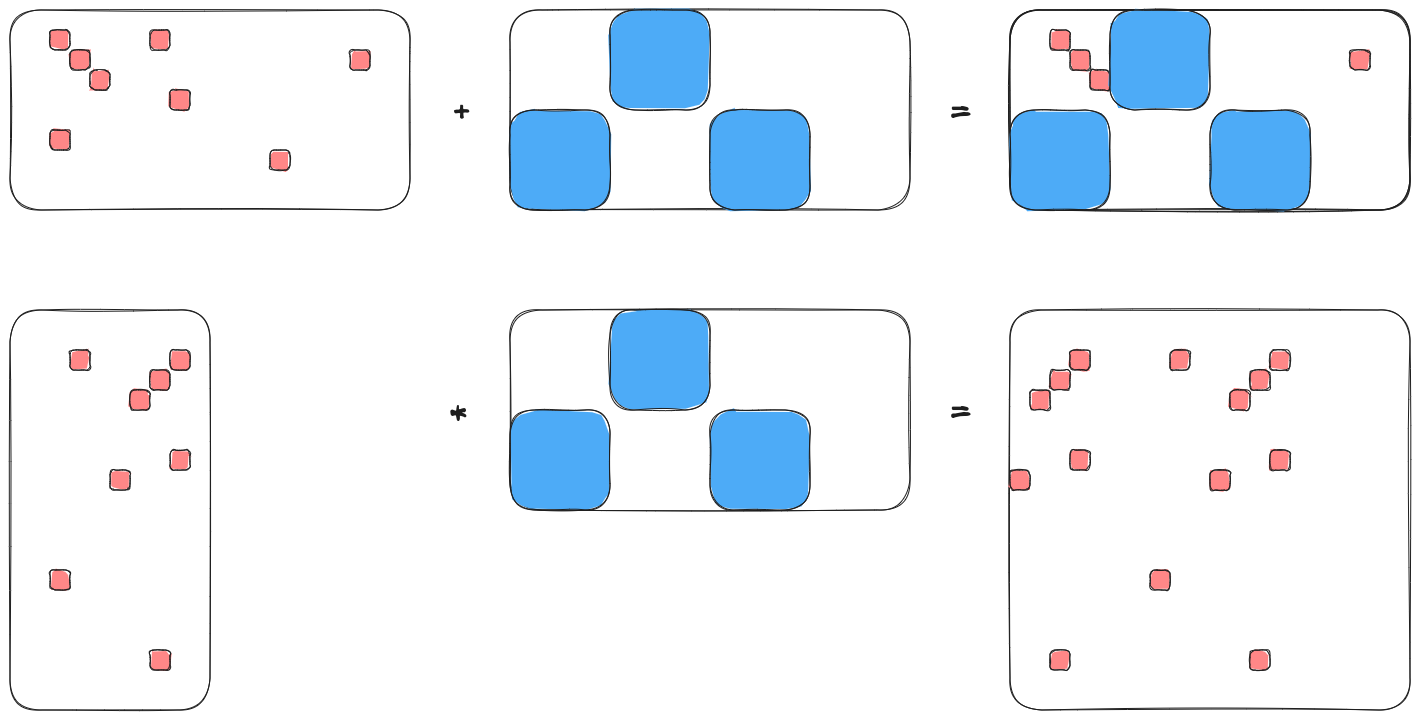
Fig. 9 An example of combining the sparsities of two 10 by 20 matrices.

Fig. 9 shows two of the basic tensor operations for two matrices \(\mathbf{A}\) and \(\mathbf{B}\), each of which is 10 by 20. In code:

Shape shape{10, 20};

Element sparse_a(
   shape, {{1,2}, {1, 7}, {2,3}, {2,17}, {3,4}, {5,8}, {7,2}, {8,13}}
);
Block sparse_b(shape,
   {shape.slice({0, 5}, {5, 10}),
    shape.slice({5, 0}, {10, 5}),
    shape.slice({5, 10}, {10, 15})}
);

// Addition
Sparsity c;
c("i,j") = a("i,j") + b("i,j");
assert(c == a.union(b));

// Contraction
c("i,j") = a("i,k") * b("k,j");
Element corr(Shape{20,20},
   {{2,3}, {2,8}, {2,13}, {3,2}, {3,12}, {4,1}, {4,11}, {7, 3}, {7,13},
    {8,0}, {8,10}, {13,7}, {18,2}, {18,12}}
);
assert(c == corr);

Composing of sparsity objects follows the same API as composing with other TensorWrapper objects, largely for consistency.

Basic Operations

Note

This section will be filled out more as the operations needed are better understood.

All sparse containers inherit from the Sparsity class, which also defines the basic API for many sparsity operations.

Sparsity s = get_tensor_sparsity();
Sparsity other_sparsity = get_other_sparsity();
// Checks if element (0,1) is 0
auto is_zero = s.is_zero({0, 1});

// Checks if a block starting with (0,1) and ending with (10, 10) is all 0
is_zero = s.is_zero({0,1}, {10, 10});

// Checks if element (0,1) is non-zero
auto is_nonzero = s.is_nonzero({0, 1});

// Checks if the block starting with (0,1) and ending with (10, 10) has any
// non-zero elements
is_nonzero = s.is_nonzero({0, 1}, {10, 10});

// Compute the sparsity (# of zero elements/total number of elements)
auto sparsity = s.sparsity();

// Create a new sparsity object with the same total shape and the non-zero
// elements from s and other_sparsity
auto the_union = s.nonzero_union(other_sparsity);

// Create a new sparsity object with the same total shape and the zero
// elements from z and other_sparsity
the_union = s.zero_union(other_sparsity);

Summary

Element Sparsity

Specifying a tensor is element sparse is done by making an instance of Element.

Block Sparsity

Specifying a tensor is block sparse is done by making an instance of Block.

Effective Sparsity

Exploiting effective sparsity is done with the Norm class.

Operational Sparsity

The Sparsity objects can be composed using Einstein notation. Sparsity can then be propagated to the result by carrying out the expressed operation.

Effective Operational Sparsity

Key to this effort is a way to estimate the result without fully computing it. Norms, are a natural solution and have been added as an optional member to the Sparsity class.

Dual problem

To account for the fact that sometimes it is easier to specify the zeros rather than the non-zeros, we have respectively introduced the Zero and Nonzero strong types.

Symmetry

The Sparsity base class holds a Symmetry object and can use it to only store the symmetry unique sparsity information/generate the symmetry redundant information.

Basic Operations

Basic operations have been factored out into the Sparsity base class. The exact API