Designing the Layout Component
This page records the process of designing the layout component of TensorWrapper.
Note
This page needs revisited when more features are implemented. In particular:
Should C++ type representation live here or in the allocator?
Similar question for the hardware backend.
Tiled vs. not tiled is actually covered by looking at the shape. If it’s nested it’s tiled (in a general sense). At the very least tiled could be a class derived from physical
What is a (tensor) layout?
Tensors contain (hyper-) rectangular arrays of elements. A layout describes the properties of the (hyper-) rectangular array including its shape, symmetry, and sparsity. Layouts can be logical (how the user wants to interact with the tensor class) or physical (how the tensor is actually stored in memory).
Why do we need a (tensor) layout?
The layout class is needed to couple the shape, symmetry, and sparsity together. Derived classes are needed to distinguish the logical and physical layouts.
Tensor Layout Considerations
- Reshape
One of the most fundamental layout considerations is being able to reshape the tensor. Reshaping is minimally needed to store tensors in memory/on disk.
Tiling a tensor is also a reshape, albeit one that increases the rank.
As tiling suggests, reshapes can be logical and need not be physical.
The sparsity and symmetry of the tensor will need to be updated to match the new shape.
TensorWrapper will store the data in objects provided by the backend, the “physical” shape TensorWrapper stores may therefore still be logical as the true physical shape is left to the backend.
Multiple vectorization strategies exist (row-major, column-major being the most natural). Even if this is handled by the backend, the backend may require us to choose.
- Representation
Elements of a tensor can have a variety of types (in a C++ sense). Even if the user provides us values in single-precision, they may want the algebra to be done in double-precision to mitigate against finite-arithmetic errors.
In theory, it is possible to have uncertainty models for each kernel which allow us to predict the error resulting from dropping precision. In practice such models are not readily available and users typically use intuition.
Representations could conceivably vary by tile.
- Ownership
Where do the literal values live? In RAM? On the GPU? On disk? Implicit via a generating function? Which process owns which tiles?
Cost to recompute tiles may vary, meaning we may want different ownership strategies per tile.
May want the same tile to be owned by multiple processes.
- Distinction
A large motivation for the layout component is simply to distinguish how the tensor is actually laid out from how the user declared it.
The classes in the layout component serve somewhat like a strong type to tell the physical/logical layouts apart (with classes in the layout component containing the actual layout).
- Basic operations
We anticipate that users will minimally want to be able to retrieve the state stored in the classes. Aside from that we anticipate use cases involving:
Composition. As tensors are composed into expressions, so too will be their layouts.
Toggle the on-the-fly nature of tiles
Change the representation/ownership
Out of Scope
- Tiling Process
The actual process of tiling a shape is assumed to be done elsewhere. The layout component will hold the resulting tiled shape.
The best tilings rely on properties of the basis set. Often these properties are not readily available to the tensor, which is why tiling will likely need to occur outside TensorWrapper for the foreseeable future.
- Backend Selection
Arguably part of laying out the tensor is also choosing the backend to hold the data. The layout component tries to factor out as many of the layout considerations as possible into a backend independent layer. The actual selection of the backend is done in the allocator component (see Designing the Allocator).
Layout Design
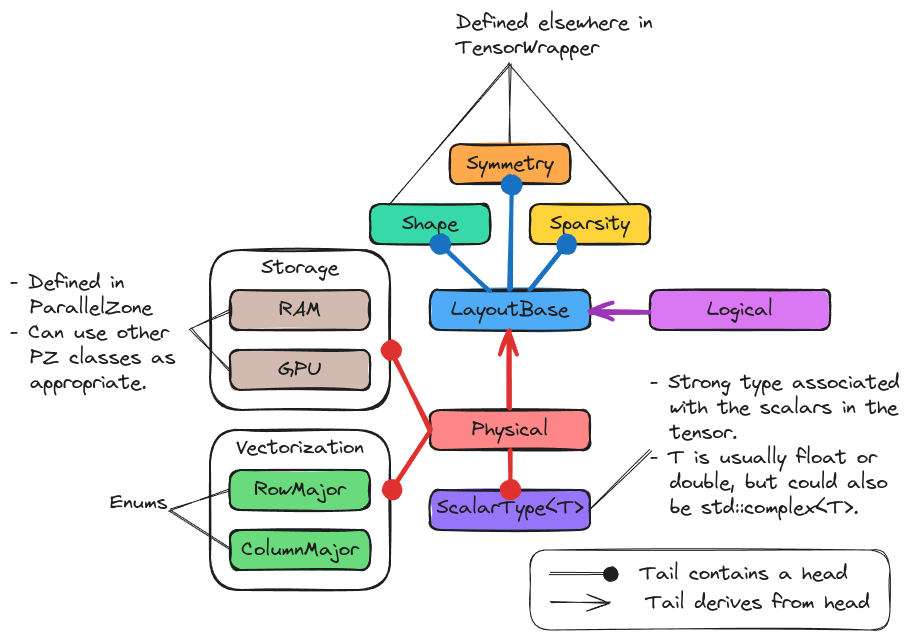
Fig. 10 The major pieces of the layout component.
Fig. 10 illustrates the major pieces of the layout component. The
base class of the component is the LayoutBase class. This class defines the
common API and contains Shape, Symmetry, and Sparsity
objects.
Proposed APIs
Since TensorWrapper will in general be used in distributed contexts we assume
that users will typically be constructing Tiled objects, which are
constructed by:
// Determining the actual shape is outside the concern of layout
auto shape = get_actual_shape();
// as is computing the symmetry and sparsity associated with it
auto [symmetry, sparsity] = update_symmetry_and_sparsity(shape);
// We anticipate that most users will create a Tiled object then set
// the tile properties
Tiled tl(shape, symmetry, sparsity);
tl.set_all_tiles(RowMajor); // All tiles will be vectorized in row-major
tl.set({0, 1}, ScalarType<float>{}); // Only tile 0,1 will use floats
tl.set({0, 1}, {10, 10}, GPU); // The {0,1} to {10,10} slice of tiles will be
// By default all tiles are stored, *i.e.*, they are NOT thrown away after
// use. To switch a tile (or tiles) to being built on-the-fly:
tl.do_not_store({0, 1});
tl.store({0, 2});
// We note that most backends do not actually support tile by tile layouts
// so the above operations are likely to lead to runtime errors when
// attempting to allocate the backend until support for mixed tile layouts
// is built into TensorWrapper itself.
By default all tiles will be stored, row major, ScalarType<double>, and RAM
based. The distribution of the tiles (which process gets which tile is left to
the backend for now, but could eventually be set by mapping
ParallelZone::ResourceSet objects to tile indices/ranges).
Declaring a MonoTile object is conceptually similar except that the set
member does not need tile indices or ranges:
// Like TiledLayout construction, shape, symmetry, and sparsity must be made
// in advance for the Layout class
auto [shape, symmetry, sparsity] = get_inputs();
MonoTile l(shape, symmetry, sparsity);
l.set(RowMajor);
l.set(ScalarType<std::complex<double>>);
l.set(GPU);
Summary
- Reshape
The
Tiledobject holds aShapeobject and is capable of storing an enum representing the vectorization strategy on a per tile basis.- Representation
The
Tiledobject holds what C++ type the scalars are on a per tile basis.- Ownership
The
Tiledobject allows the user to specify what process owns each tile, as well as where the tile is stored (e.g., RAM, disk, or GPU), and if it is even stored.- Distinction
This consideration is addressed by the existence of the
TiledandMonoTileclasses.- Basic operations
The API examples above demonstrate how users can perform the considered operations.